Boa tarde, desde já agradeço a ajuda que me deram em outro tópico,se puderem dar umas dicas nesse exercício também ficava muito agradecido..
Precisava de umas dicas para os 2, o livro explica muito sinteticamente.
Obrigado.





 . Seja o conjunto
. Seja o conjunto 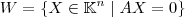 .
. , temos que analisar as três condições abaixo.
, temos que analisar as três condições abaixo.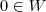 .
. temos que
temos que 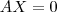 .
.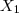 e
e  pertencem a W, então
pertencem a W, então  pertence a W .
pertence a W .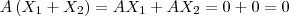
 pertence a
pertence a  , então
, então  pertence a W.
pertence a W.
 .
.
LuizAquino escreveu:Para o primeiro exercício, basta seguir as instruções de Fantini.
Para o segundo, é só testar as três condições que caracterizam um subespaço.
Considere uma matriz. Seja o conjunto
.
Para verificar se W é subespaço de, temos que analisar as três condições abaixo.
(i).
Essa condição é verdadeira, pois paratemos que
.
Obs.: note que o símbolo "0" não é o número zero, mas sim uma matriz nula de tamanho n por 1.
(ii) See
pertencem a W, então
pertence a W .
Essa condição é verdadeira, pois temos que:
(iii) Se X pertence a W epertence a
, então
pertence a W.
Essa condição é verdadeira, pois temos que:
Logo, como (i), (ii) e (iii) são verdadeiras, temos que W é subespaço de.
Observação
Nos seus próximos tópicos, escreva todo o texto do exercício. Não envie o texto como uma imagem, pois isso prejudica o sistema de busca do fórum.

Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes

 .
.
 :
: