 por cortes » Ter Mai 26, 2009 20:54
por cortes » Ter Mai 26, 2009 20:54
[tex]\lim_{x\rightarrow - 1} {x}^{2} - 1 /{7}^{x3}+{2}^{x2}-5x
Boa noite
Estou com duvida na resoluçao deste limite, ja tentei por divisão de polinomios e formula de bascara e nao chego a um resultado alguem pode me ajudar?
Editado pela última vez por
cortes em Ter Mai 26, 2009 21:33, em um total de 5 vezes.
-
cortes
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Seg Mai 25, 2009 23:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: contabeis
- Andamento: cursando
 por Molina » Ter Mai 26, 2009 21:07
por Molina » Ter Mai 26, 2009 21:07
Boa noite e bem-vindo, cortes.
Se possível, expresse seu limite utilizando o editor LaTeX.
Há um tópico sobre o uso dele que pode exclarecer todas as suas dúvidas.
Assim ficará mais fácil dos outros entenderem seu problema, já que não dá pra ter nem idém a que valor x está tendendo.
Estou a suas ordens, abraços!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por cortes » Ter Mai 26, 2009 21:31
por cortes » Ter Mai 26, 2009 21:31
cortes escreveu:[tex]\lim_{x\rightarrow - 1} {x}^{2} - 1 /{7}^{x3}+{2}^{x2}-5x
Boa noite
Estou com duvida na resoluçao deste limite, ja tentei por divisão de polinomios e formula de bascara e nao chego a um resultado alguem pode me ajudar?
-
cortes
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Seg Mai 25, 2009 23:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: contabeis
- Andamento: cursando
 por Molina » Ter Mai 26, 2009 21:36
por Molina » Ter Mai 26, 2009 21:36
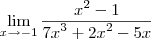
Este aqui é o limite que você deseja descobrir, correto?
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por cortes » Ter Mai 26, 2009 21:41
por cortes » Ter Mai 26, 2009 21:41
Este mesmo.
-
cortes
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Seg Mai 25, 2009 23:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: contabeis
- Andamento: cursando
 por Molina » Ter Mai 26, 2009 21:55
por Molina » Ter Mai 26, 2009 21:55
Certo.
Você viu que dividindo todos os termos por

e substituindo x por -1, ficariamos com uma ideterminação do tipo

.
Nestes casos, podemos usar uma regra chamada L'Hopital, porém, tem que conhecer derivada para usa-la.
Você já estudou (ou está estudando) deriavada?

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por cortes » Ter Mai 26, 2009 21:58
por cortes » Ter Mai 26, 2009 21:58
Sim verifiquei que o resultado da uma indeterminação.
Estou tbm estudando derivada.
-
cortes
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Seg Mai 25, 2009 23:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: contabeis
- Andamento: cursando
 por Molina » Ter Mai 26, 2009 22:02
por Molina » Ter Mai 26, 2009 22:02
Beleza então.
NEste caso você pode usar L'Hopital.
Consiste em pegar a expressão do numerador e derivar; pegar a expressão do numerador e derivar tambem. Faça isso até acabar com a indeterminação do tipo zero sobre zero ou infinito sobre infinito.
Caso você faça uma vez e não caia numa indeterminação, basta substituir x por -1 e encontrará o limite.
Faz aí e qualquer novidade é só postar.
Abraços!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por cortes » Ter Mai 26, 2009 22:08
por cortes » Ter Mai 26, 2009 22:08
Voce diz fatorar ?
Ja fiz isso.
-
cortes
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Seg Mai 25, 2009 23:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: contabeis
- Andamento: cursando
 por Molina » Ter Mai 26, 2009 22:41
por Molina » Ter Mai 26, 2009 22:41
cortes escreveu:Voce diz fatorar ?
Ja fiz isso.
Não, eu digo em fazer a derivada de
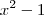
e a derivada

Depois de derivar essas duas expressões você substitui -1 no lugar do x.
O resultado que você irá obter é o limite que você estava procurando.
Caso não entenda ainda o que é L'Hopital sugiro ler: pt.wikipedia.org/wiki/Regra_de_l'Hôpital
Abraços,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por cortes » Ter Mai 26, 2009 22:46
por cortes » Ter Mai 26, 2009 22:46
minhas resposta esta dando -1/6 nao sei se esta certo
Fiz o seguinte:

substitui

por

depois achei as raiz x' e x" e substitui na formula mas nao sei se esta certo
-
cortes
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Seg Mai 25, 2009 23:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: contabeis
- Andamento: cursando
 por cortes » Ter Mai 26, 2009 22:47
por cortes » Ter Mai 26, 2009 22:47
vou ler o conteudo indicado
-
cortes
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Seg Mai 25, 2009 23:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: contabeis
- Andamento: cursando
 por Molina » Ter Mai 26, 2009 22:57
por Molina » Ter Mai 26, 2009 22:57
Sim. Deu a mesma resposta que a minha, usando L'Hopital.
Derivada de x^2 - 1 = 2x - 0
Derivada de 7x^3+2x^2-5x = 21x^2+4x-5

Bom estudo,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por cortes » Ter Mai 26, 2009 23:05
por cortes » Ter Mai 26, 2009 23:05
obrigada
-
cortes
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Seg Mai 25, 2009 23:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: contabeis
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] Gráfico e limite para função maior inteiro
 por Raphaela_sf » Qui Abr 05, 2012 19:26
por Raphaela_sf » Qui Abr 05, 2012 19:26
- 1 Respostas
- 6641 Exibições
- Última mensagem por LuizAquino

Qui Abr 05, 2012 20:53
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções reais de várias variáveis
por Bianca_R » Dom Nov 04, 2012 17:17
- 1 Respostas
- 4786 Exibições
- Última mensagem por MarceloFantini

Dom Nov 04, 2012 19:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite trigonométrico] Como calculo este limite?
por Ronaldobb » Qua Nov 07, 2012 23:14
- 3 Respostas
- 5117 Exibições
- Última mensagem por Ronaldobb

Qui Nov 08, 2012 07:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] limite trigonométrico quando x tende ao infinito
por Ge_dutra » Seg Jan 28, 2013 10:13
- 2 Respostas
- 7256 Exibições
- Última mensagem por Ge_dutra

Ter Jan 29, 2013 14:20
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções piso (maior inteiro)
por ViniciusAlmeida » Sáb Fev 14, 2015 10:09
- 2 Respostas
- 4434 Exibições
- Última mensagem por adauto martins

Qui Fev 19, 2015 15:01
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.






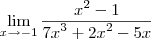


 e substituindo x por -1, ficariamos com uma ideterminação do tipo
e substituindo x por -1, ficariamos com uma ideterminação do tipo  .
.





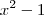 e a derivada
e a derivada 



 por
por 






![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.