 por renato9 » Dom Dez 25, 2011 15:27
por renato9 » Dom Dez 25, 2011 15:27
Como resolver equações modulares quando existem duas "parcelas"? Tentei usar a definição de módulo, mas acho que não é o método mais adequado.
Segue a equação-exemplo:
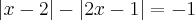
-
renato9
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Dom Dez 25, 2011 15:18
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por fraol » Dom Dez 25, 2011 20:24
por fraol » Dom Dez 25, 2011 20:24
Olá Renato,
Uma forma de você resolver seria por intermédio da construção do gráfico de cada uma das funções e verificar os

nos quais ocorre a intersecção dos gráficos, mas pela definição também sai, tem que sair, só que deve-se aplicá-la duas vezes, uma para cada equação modular, vamos obter assim 4 equações, depois de resolvê-las validamos as respostas eliminando, eventualmente, as que não satisfazem a equação original.
Valeu?
Francisco.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por renato9 » Dom Dez 25, 2011 21:42
por renato9 » Dom Dez 25, 2011 21:42
Obrigado pela atenção, Francisco.
Resolvendo, fiz o seguinte:


Mas deve haver algum erro, pois do resultado,
somente um elemento ( ) serve como solução
) serve como solução, contrariando, assim, o gabarito oficial, que coloca na resposta a existência de
dois elementos como solução, com

. Há algum erro no procedimento?
Grato.
-
renato9
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Dom Dez 25, 2011 15:18
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por fraol » Dom Dez 25, 2011 22:08
por fraol » Dom Dez 25, 2011 22:08
Apliquei a definição em

da seguinte forma:
(1a)

(1b)

(2a)

(2b)
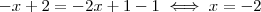
Testando os valores encontrados vemos que a solução é
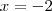
ou
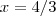
O que você acha?
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por renato9 » Dom Dez 25, 2011 22:14
por renato9 » Dom Dez 25, 2011 22:14
Pensei nisso e havia achado também o

. O problema é que se houvesse três ou mais "parcelas", tornaria o processo bastante trabalhoso.
Alguma sugestão em relação a isso?
Obrigado.
-
renato9
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Dom Dez 25, 2011 15:18
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por fraol » Dom Dez 25, 2011 22:29
por fraol » Dom Dez 25, 2011 22:29
Oi Renato,
Não vejo saída nesses casos, ou plotamos as funções modulares num software e pegamos as intersecções ou desenvolvemos as equações através da aplicação da definição - nesses casos serão
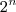
equações, sendo

o número de módulos na expressão original.
Se algum outro colega que nos lê tiver alguma alternativa manda pra gente.
Abç,
Francisco.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por renato9 » Dom Dez 25, 2011 22:39
por renato9 » Dom Dez 25, 2011 22:39
É isso, Francisco. A utilização da definição em casos de mais parcelas seria inviável na ocasião de uma prova com muitas questões e pouco tempo. É bastante possível para essa questão, no entanto. Obrigado pela ajuda e vamos aguardar alguma sugestão de outro colega.
Abraços.
-
renato9
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Dom Dez 25, 2011 15:18
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Equação Modular] com equação de 2º grau
por paola-carneiro » Qui Abr 05, 2012 15:53
- 2 Respostas
- 3418 Exibições
- Última mensagem por paola-carneiro

Sex Abr 06, 2012 16:23
Funções
-
- Equação modular
por amandactdas » Qui Jul 23, 2009 13:14
- 1 Respostas
- 2800 Exibições
- Última mensagem por Molina

Qui Jul 23, 2009 15:26
Funções
-
- Equação modular.
por JoaoGabriel » Sáb Set 18, 2010 11:01
- 3 Respostas
- 2514 Exibições
- Última mensagem por JoaoGabriel

Sáb Set 18, 2010 14:00
Funções
-
- Equação Modular
 por baianinha » Ter Mai 24, 2011 22:15
por baianinha » Ter Mai 24, 2011 22:15
- 2 Respostas
- 1955 Exibições
- Última mensagem por LuizAquino

Sex Mai 27, 2011 22:05
Sistemas de Equações
-
- Equação Modular
por Rafael16 » Dom Mar 04, 2012 14:07
- 3 Respostas
- 2143 Exibições
- Última mensagem por LuizAquino

Seg Mar 05, 2012 14:23
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
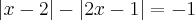

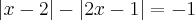

 nos quais ocorre a intersecção dos gráficos, mas pela definição também sai, tem que sair, só que deve-se aplicá-la duas vezes, uma para cada equação modular, vamos obter assim 4 equações, depois de resolvê-las validamos as respostas eliminando, eventualmente, as que não satisfazem a equação original.
nos quais ocorre a intersecção dos gráficos, mas pela definição também sai, tem que sair, só que deve-se aplicá-la duas vezes, uma para cada equação modular, vamos obter assim 4 equações, depois de resolvê-las validamos as respostas eliminando, eventualmente, as que não satisfazem a equação original.


 ) serve como solução, contrariando, assim, o gabarito oficial, que coloca na resposta a existência de dois elementos como solução, com
) serve como solução, contrariando, assim, o gabarito oficial, que coloca na resposta a existência de dois elementos como solução, com  . Há algum erro no procedimento?
. Há algum erro no procedimento?
 da seguinte forma:
da seguinte forma:


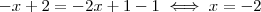
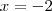 ou
ou 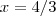

 . O problema é que se houvesse três ou mais "parcelas", tornaria o processo bastante trabalhoso.
. O problema é que se houvesse três ou mais "parcelas", tornaria o processo bastante trabalhoso.
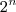 equações, sendo
equações, sendo  o número de módulos na expressão original.
o número de módulos na expressão original.


 .
.



