 por Adriana Barbosa » Ter Mai 26, 2009 21:59
por Adriana Barbosa » Ter Mai 26, 2009 21:59
Caucula:
f(x)= x²-3x+2, f(0), f(a+1), e
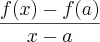
se x

a
Minha resolução:
f(0)=0²-3*0+2=2
f(a+1)= (a+1)²-3(a+1)+2=
a²+2aa+1-3a-3+2=
a²-a
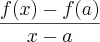
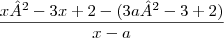

(x-a)-3(x-a)
Só consegui até aqui!
A resposta da x+a-3!
Podem me ajudar???
-
Adriana Barbosa
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Ter Mai 26, 2009 21:45
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Química
- Andamento: cursando
 por Molina » Ter Mai 26, 2009 22:32
por Molina » Ter Mai 26, 2009 22:32
Boa noite, Adriana.
Só uma pequena correção (provavelmente de digitação) na segunda linha:
Adriana Barbosa escreveu:f(a+1)= (a+1)²-3(a+1)+2=
a²+2aa+1-3a-3+2=
a²-a
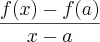

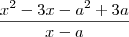
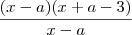
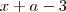
Bom estudo,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Adriana Barbosa » Ter Mai 26, 2009 23:27
por Adriana Barbosa » Ter Mai 26, 2009 23:27
Isso mesmo, erro de digitação!
É que estou tendo um pouquinho de dificuldades em digitar!
Obrigada!
Mas por favor, como posso continuar minha resolução?
Estou indo no caminho correto?
Obrigada
-
Adriana Barbosa
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Ter Mai 26, 2009 21:45
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Química
- Andamento: cursando
 por Molina » Ter Mai 26, 2009 23:41
por Molina » Ter Mai 26, 2009 23:41
Bom, eu já coloquei o modo certo de resolver aquela que você estava com dificuldades de terminar. Acho que você fez algumas operações equivocadas. Caso não entenda algum procedimento que eu tomei, é só perguntar.
Abraços,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Função e Operação com Função
 por Adriana Barbosa » Ter Mai 26, 2009 22:23
por Adriana Barbosa » Ter Mai 26, 2009 22:23
- 2 Respostas
- 1509 Exibições
- Última mensagem por Adriana Barbosa

Ter Mai 26, 2009 23:29
Funções
-
- Operação básica
por Fernanda Lauton » Qui Jun 17, 2010 15:40
- 11 Respostas
- 6461 Exibições
- Última mensagem por Fernanda Lauton

Seg Jun 21, 2010 18:13
Álgebra Elementar
-
- Operação de conjuntos
por marcio277 » Qui Set 09, 2010 15:29
- 1 Respostas
- 3593 Exibições
- Última mensagem por MarceloFantini

Qui Set 09, 2010 17:46
Álgebra Elementar
-
- Operação com Matriz
por DanielRJ » Qui Set 09, 2010 16:04
- 2 Respostas
- 1888 Exibições
- Última mensagem por DanielRJ

Qui Set 09, 2010 17:41
Matrizes e Determinantes
-
- [operação com frações simples]
por Aprendiz2012 » Seg Ago 20, 2012 20:07
- 1 Respostas
- 1369 Exibições
- Última mensagem por Cleyson007

Ter Ago 21, 2012 10:23
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
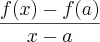 se x
se x a
a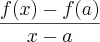
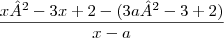


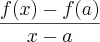 se x
se x a
a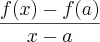
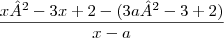


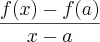

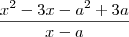
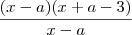
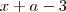










 .
.



