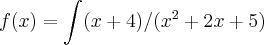


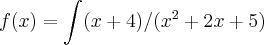

Marcio Cristo escreveu:Boa tarde , como ficaria a seguinte integral? A minha duvida é por onde começar e como ficaria a fatoração do polinomio que está no denominador . Se puder fazer um passo a passo . Agradeço desde ja.
integrate (x+4)/(x^2+2x+5) dx


Marcio Cristo escreveu:noto que x+4/x^2+2x+5 foi reescrito na forma de 2x+2 / 2( x^2+2x+5) + 3/x^2+2x+5 , qual a tecnica usada para essa transformação de polinomios ???
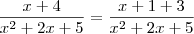
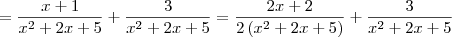


Marcio Cristo escreveu:qual a finalidade de ter multiplicado a primeira expressão toda por 2 ?? não poderia integrar com aquele polinomio x+1 ??
 e
e 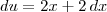 , temos que :
, temos que :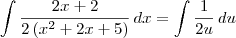
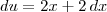 como sendo
como sendo 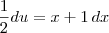 . Nesse caso, podemos escrever diretamente que:
. Nesse caso, podemos escrever diretamente que: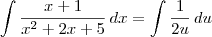

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)