 por DanielRJ » Dom Dez 18, 2011 15:23
por DanielRJ » Dom Dez 18, 2011 15:23
Dado

,

,
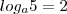
o valor da expressão
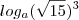
é igual a:
resposta: -3
Minha tentativa:
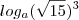

![3[log_{a}\sqrt{3}+log_{a}\sqrt{5}] 3[log_{a}\sqrt{3}+log_{a}\sqrt{5}]](/latexrender/pictures/1b60fc9abac0f20e90dbc3203c245659.png)
![3[\frac{1}{2}log_{a}3+\frac{1}{2}log_{a}5] 3[\frac{1}{2}log_{a}3+\frac{1}{2}log_{a}5]](/latexrender/pictures/b65cdd4ce935c3ae179aa16323702532.png)
substituindo os valores:
![3[\frac{-1}{2}+\frac{2}{2}] 3[\frac{-1}{2}+\frac{2}{2}]](/latexrender/pictures/f9597277f5a0af9807604a315c220659.png)
![3[\frac{1}{2}] 3[\frac{1}{2}]](/latexrender/pictures/d5ab1286d1245145773dd976049720fa.png)

Onde errei?
-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Dom Dez 18, 2011 17:41
por MarceloFantini » Dom Dez 18, 2011 17:41
Não está errado. Se fosse

ao invés de

então bateria com a resposta.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Questão POSCOMP 2011] Ajuda para interpretar questão
por hlustosa » Dom Jul 29, 2012 14:54
- 3 Respostas
- 12985 Exibições
- Última mensagem por hlustosa

Seg Jul 30, 2012 01:13
Funções
-
- Questão de P.A.
por mushthielv » Seg Ago 17, 2009 12:21
- 2 Respostas
- 10965 Exibições
- Última mensagem por Elcioschin

Ter Ago 18, 2009 08:54
Progressões
-
- QUESTÃO
por GABRIELA » Ter Set 08, 2009 16:32
- 2 Respostas
- 15107 Exibições
- Última mensagem por GABRIELA

Ter Set 08, 2009 21:21
Matrizes e Determinantes
-
- Questão da FCC
por wanderlymarques » Qua Nov 18, 2009 12:44
- 2 Respostas
- 5022 Exibições
- Última mensagem por wanderlymarques

Qui Nov 19, 2009 12:58
Cálculo: Limites, Derivadas e Integrais
-
- questão
por sirle ignes » Seg Mar 08, 2010 23:46
- 2 Respostas
- 4790 Exibições
- Última mensagem por sirle ignes

Ter Mar 09, 2010 17:32
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 ,
, ,
, 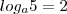
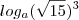 é igual a:
é igual a: 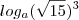

![3[log_{a}\sqrt{3}+log_{a}\sqrt{5}] 3[log_{a}\sqrt{3}+log_{a}\sqrt{5}]](/latexrender/pictures/1b60fc9abac0f20e90dbc3203c245659.png)
![3[\frac{1}{2}log_{a}3+\frac{1}{2}log_{a}5] 3[\frac{1}{2}log_{a}3+\frac{1}{2}log_{a}5]](/latexrender/pictures/b65cdd4ce935c3ae179aa16323702532.png)
![3[\frac{-1}{2}+\frac{2}{2}] 3[\frac{-1}{2}+\frac{2}{2}]](/latexrender/pictures/f9597277f5a0af9807604a315c220659.png)
![3[\frac{1}{2}] 3[\frac{1}{2}]](/latexrender/pictures/d5ab1286d1245145773dd976049720fa.png)


 ,
, ,
, 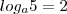
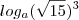 é igual a:
é igual a: 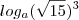

![3[log_{a}\sqrt{3}+log_{a}\sqrt{5}] 3[log_{a}\sqrt{3}+log_{a}\sqrt{5}]](/latexrender/pictures/1b60fc9abac0f20e90dbc3203c245659.png)
![3[\frac{1}{2}log_{a}3+\frac{1}{2}log_{a}5] 3[\frac{1}{2}log_{a}3+\frac{1}{2}log_{a}5]](/latexrender/pictures/b65cdd4ce935c3ae179aa16323702532.png)
![3[\frac{-1}{2}+\frac{2}{2}] 3[\frac{-1}{2}+\frac{2}{2}]](/latexrender/pictures/f9597277f5a0af9807604a315c220659.png)
![3[\frac{1}{2}] 3[\frac{1}{2}]](/latexrender/pictures/d5ab1286d1245145773dd976049720fa.png)


 ao invés de
ao invés de  então bateria com a resposta.
então bateria com a resposta.


