Usando a propriedade arquimediana, prove que se
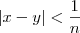 para todo
para todo 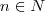 , então
, então 

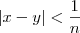 para todo
para todo 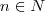 , então
, então 

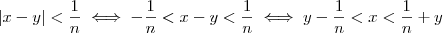
 o que é sempre verdade para qualquer
o que é sempre verdade para qualquer  real e nada concluímos.
real e nada concluímos. então ficaremos com
então ficaremos com  e portanto
e portanto  .
.
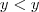 não faz muito sentido.
não faz muito sentido.


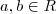 tais que
tais que  então existe algum
então existe algum  tal que
tal que 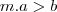 .
. , invertendo ficamos com
, invertendo ficamos com 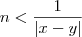 .
.  tal que
tal que  .
. em (3) só existirá se
em (3) só existirá se 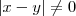

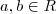 tais que
tais que  então existe algum
então existe algum  tal que
tal que 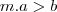 .
. . Vamos supor então que
. Vamos supor então que  e portanto
e portanto  .
. tal que
tal que  .
. então
então  também, chamemos esse produto de
também, chamemos esse produto de  .
. e
e 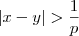 . Ambos
. Ambos  e
e  naturais quaisquer contrariando a hipótese dada no enunciado original e a nossa suposição de que
naturais quaisquer contrariando a hipótese dada no enunciado original e a nossa suposição de que  .
. .
.  } é igual a 0 (usando a Arquimediana). E daí usaríamos limites, mas aí estaríamos usando outros recursos além da Arquimediana.
} é igual a 0 (usando a Arquimediana). E daí usaríamos limites, mas aí estaríamos usando outros recursos além da Arquimediana.
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.