 por LuizAquino » Sex Dez 02, 2011 18:36
por LuizAquino » Sex Dez 02, 2011 18:36
paula luna escreveu:Oi estou com muita dificuldade com esta questao, se alguem conseguir resolve-la por favor poste a resoluçao. Segue abaixo a questao com resposta e tambem o que eu tentei.
Questao:
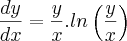
Resposta:
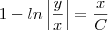
paula luna escreveu:Minha tentativa: Bem, antes de botar as expressoes eu queria tambem perguntar se esta questao tambem nao poderia ser feita por 'variaveis separaveis' diretamente.
Não poderia.
Ok.
paula luna escreveu:Arrumando...
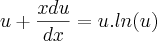
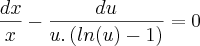
Ok.
paula luna escreveu:Aplicando a integral nos 2 lados:
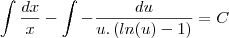
Calculando ...
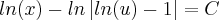
Apenas corrigindo:
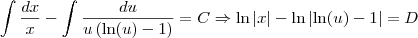 Obs. 1:
Obs. 1: Lembre-se que ao calcular as duas integrais surgirão duas novas constantes, que irão subtrair
C dando origem a uma outra constante
D.
paula luna escreveu:Daqui pra frente eu usei propriedade de log e exponencial pra tranfsrmar a subtraçao de logs em divisao e poder retirar uma das logs ( meio confuso mas acho que da pra intender aqui embaixo)
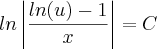
Errado. O correto seria:
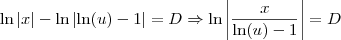
Disso temos que:
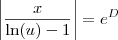
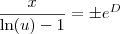
Note que
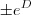
é uma constante. Vamos chamá-la de
E.
Desse modo, temos que:
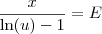
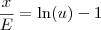
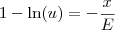
Lembrando que
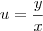
e chamando a constante
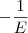
de
F , temos que:
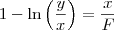 Obs. 2:
Obs. 2: Vale lembrar que o "nome" que damos as constantes não importa. A cada passo você pode chamá-las de tal modo que no fim a resposta fique no formato do gabarito.
Obs. 3: Da forma como foi apresentada a EDO, devemos ter
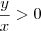
, pois essa expressão está dentro do logaritmo que aparece no segundo membro da equação. Portanto, na resposta final essa expressão não precisa aparecer em módulo.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por paula luna » Dom Dez 04, 2011 16:12
por paula luna » Dom Dez 04, 2011 16:12
-
paula luna
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Qui Mai 05, 2011 21:56
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equações diferenciais
por tiagofabre » Sex Set 21, 2012 00:48
- 1 Respostas
- 1861 Exibições
- Última mensagem por MarceloFantini

Sex Set 21, 2012 01:14
Cálculo: Limites, Derivadas e Integrais
-
- equacoes diferenciais
por Thais Bomfim » Qua Dez 12, 2012 01:58
- 2 Respostas
- 2192 Exibições
- Última mensagem por Thais Bomfim

Qua Dez 12, 2012 14:02
Equações
-
- Equações Diferenciais
por sergio2205 » Qua Mar 06, 2013 13:27
- 1 Respostas
- 1736 Exibições
- Última mensagem por Russman

Qua Mar 06, 2013 15:14
Equações
-
- Equações Diferenciais
por marinalcd » Sex Ago 09, 2013 15:19
- 1 Respostas
- 1633 Exibições
- Última mensagem por Man Utd

Dom Jun 15, 2014 17:40
Cálculo: Limites, Derivadas e Integrais
-
- Equações Diferenciais
por FernandaOliveira » Dom Ago 25, 2013 20:42
- 1 Respostas
- 1666 Exibições
- Última mensagem por FernandaOliveira

Qua Ago 28, 2013 16:41
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
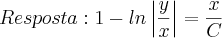
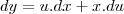
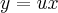
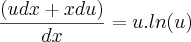
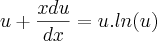
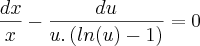
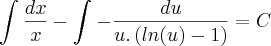
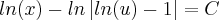
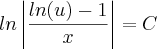
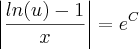
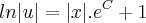
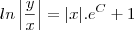
 por quem leu, quem tentou, quem conseguiu ....
por quem leu, quem tentou, quem conseguiu ....


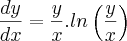
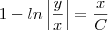
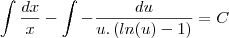
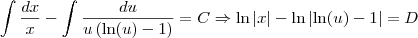
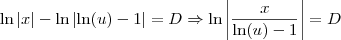
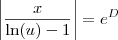
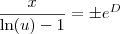
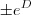 é uma constante. Vamos chamá-la de
é uma constante. Vamos chamá-la de 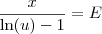
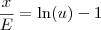
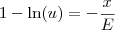
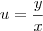 e chamando a constante
e chamando a constante 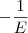 de
de 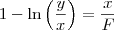
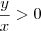 , pois essa expressão está dentro do logaritmo que aparece no segundo membro da equação. Portanto, na resposta final essa expressão não precisa aparecer em módulo.
, pois essa expressão está dentro do logaritmo que aparece no segundo membro da equação. Portanto, na resposta final essa expressão não precisa aparecer em módulo.

 , avisa que eu resolvo.
, avisa que eu resolvo.

