Seguinte, estou com um problema com uma demonstração, comecei mas fiquei "preso" em um ponto e aí vem a dúvida, estaria certo o que eu escrevi ?? Ou abordei de maneira errada o problema e por isso parei no ponto em questão ??? Segue o problema e a demonstração, ficarei imensamente grato se alguém verificasse para mim.
Problema:
Sejam A e B operadores auto-adjuntos tais que AB = BA. Mostre que existe uma única base ortonormal que diagonaliza simultaneamente A e B.
Demonstração que escrevi e parei:
Como AB = BA então A e B são operadores comutativos. Tenhamos
 um autovalor de A e
um autovalor de A e  o auto-espaço associado. Seja
o auto-espaço associado. Seja  tal que:
tal que: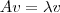
Então
 é invariante por B. Daí concluímos que v é um autovetor comum a A e a B, então:
é invariante por B. Daí concluímos que v é um autovetor comum a A e a B, então: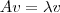

-----------------------------------------------
Eu acho que estou errando aqui, pois eu resolvi assumir um vetor
 tal que
tal que 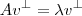
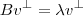
Daí eu concluo que
 pertence a uma base ortonormal... Parece que estou "forçando a barra" e por isso me soa como errado...
pertence a uma base ortonormal... Parece que estou "forçando a barra" e por isso me soa como errado...Alguém poderia me ajudar com essa demonstração ??
Desde já grato...
Renato.


 dois operadores auto-adjuntos tais que AB = BA, tenhamos
dois operadores auto-adjuntos tais que AB = BA, tenhamos 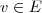 vetor não nulo tal que:
vetor não nulo tal que:
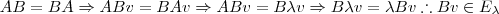
 tal que:
tal que: e
e  são ambos não invertíveis e como:
são ambos não invertíveis e como:
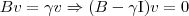
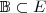 ortonormal de autovetores de A e B, logo a base
ortonormal de autovetores de A e B, logo a base  diagonaliza A e B simultaneamente.
diagonaliza A e B simultaneamente.![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)