 por rhodry » Qua Nov 30, 2011 14:14
por rhodry » Qua Nov 30, 2011 14:14

- Imagem_Exercício
olá pessoal, não consegui compreender este exercício, não sei nem por onde começar, desde já agradeço se tiver alguém disponível para me ajudar... a imagem encontra-se em anexo...
Considere duas circunferências de raios iguais a Re centro em C1 e C2 , conforme a figura abaixo. Sabendo que a distância entre C1 e C2 é dada por 2s ( 0 ? s ? R ) e que o ângulo AC2B=?,
a) Obtenha a expressão que fornece a área superposta
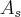
das duas circunferência em função de R,s e

-
rhodry
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Ter Out 25, 2011 17:59
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por rhodry » Qua Nov 30, 2011 15:16
por rhodry » Qua Nov 30, 2011 15:16
olá, pessoal tenho pensado da seguinte maneira..
tendo como expressão:
A=

(

-sen

)
não sei se está certo, tenho muitas dúvidas.
-
rhodry
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Ter Out 25, 2011 17:59
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por Rosana Vieira » Qua Nov 30, 2011 17:56
por Rosana Vieira » Qua Nov 30, 2011 17:56
Estou com dificuldade para resolver este exercício também
Considere duas circunferências de raios iguais a e centro em C1 e C2 , conforme a figura abaixo. Sabendo que a distância entre C1 e C2 é dada por ( ) e que o ângulo ,
a) Obtenha a expressão que fornece a área superposta das duas circunferências em função de .
b) Qual a posição relativa das circunferências quando ? Justifique utilizando a expressão obtida em a).
c ) Qual a posição relativa das circunferências quando ? Justifique utilizando a expressão obtida em a).
-
Rosana Vieira
- Usuário Parceiro

-
- Mensagens: 74
- Registrado em: Qui Nov 17, 2011 00:11
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por ivanfx » Qua Nov 30, 2011 18:20
por ivanfx » Qua Nov 30, 2011 18:20
Que tal pensarem em primeiro determinar a área do setor e depois determinar a área do triângulo retângulo que é formado traçando um segmento de C1 até C2 ai fica mais fácil para definir a fórmula
-
ivanfx
- Usuário Dedicado

-
- Mensagens: 43
- Registrado em: Dom Out 16, 2011 00:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
 por vanessa_mat » Qua Nov 30, 2011 19:01
por vanessa_mat » Qua Nov 30, 2011 19:01
Considere duas circunferências de raios iguais a R e centro em C1 e C2 , conforme a figura abaixo. Sabendo que a distância entre C1 e C2 é dada por 2s ( 0?s?R ) e que o ângulo A(C_2 ) ?B=?,
Considere duas circunferências de raios iguais a R e centro em C1 e C2 , conforme a figura abaixo. Sabendo que a distância entre C1 e C2 é dada por 2s ( 0?s?R ) e que o ângulo A(C_2 ) ?B=?,
a) Obtenha a expressão que fornece a área superposta
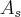
das duas circunferência em função de R,s e

[/quote]
A letra a, depois de muitas tentativas e por enquanto uma noite sem dormir fiz achando a área do setor circular menos a área do triangulo, esse resultado vezes dois:: ficou uma sopa de letrinhas, mas a intenção era essa!!! agora não estou conseguindo resolver o item b e c . Será que alguém pode me dar uma ajudinha???? Já teho a expressão do item a, mas não entendi como proceder nos itens seguintes!!!
b)Qual a posição relativa das circunferências quando A_s=0? Justifique utilizando a expressão obtida em a).
c)Qual a posição relativa das circunferências quando A_s=?R^2? Justifique utilizando a expressão obtida em a).
-
vanessa_mat
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Seg Nov 21, 2011 16:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por Rosana Vieira » Qua Nov 30, 2011 19:41
por Rosana Vieira » Qua Nov 30, 2011 19:41
vanessa_mat escreveu:Considere duas circunferências de raios iguais a R e centro em C1 e C2 , conforme a figura abaixo. Sabendo que a distância entre C1 e C2 é dada por 2s ( 0?s?R ) e que o ângulo A(C_2 ) ?B=?,
Considere duas circunferências de raios iguais a R e centro em C1 e C2 , conforme a figura abaixo. Sabendo que a distância entre C1 e C2 é dada por 2s ( 0?s?R ) e que o ângulo A(C_2 ) ?B=?,
a) Obtenha a expressão que fornece a área superposta
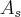
das duas circunferência em função de R,s e

A letra a, depois de muitas tentativas e por enquanto uma noite sem dormir fiz achando a área do setor circular menos a área do triangulo, esse resultado vezes dois:: ficou uma sopa de letrinhas, mas a intenção era essa!!! agora não estou conseguindo resolver o item b e c . Será que alguém pode me dar uma ajudinha???? Já teho a expressão do item a, mas não entendi como proceder nos itens seguintes!!!
b)Qual a posição relativa das circunferências quando A_s=0? Justifique utilizando a expressão obtida em a).
c)Qual a posição relativa das circunferências quando A_s=?R^2? Justifique utilizando a expressão obtida em a).[/quote]
Vanessa na atividade 2a é esta fórmula A= R2 (? – sem ?)
-
Rosana Vieira
- Usuário Parceiro

-
- Mensagens: 74
- Registrado em: Qui Nov 17, 2011 00:11
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por dea74 » Qua Nov 30, 2011 19:46
por dea74 » Qua Nov 30, 2011 19:46
ivanfx escreveu:Que tal pensarem em primeiro determinar a área do setor e depois determinar a área do triângulo retângulo que é formado traçando um segmento de C1 até C2 ai fica mais fácil para definir a fórmula
Oi Ivan
Só nao consegui enxergar o triangulo. Poderia ser mais explicito?
Abs
Déa
-
dea74
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qua Nov 30, 2011 19:22
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Licenciatura em matemática
- Andamento: formado
 por ivanfx » Qua Nov 30, 2011 20:19
por ivanfx » Qua Nov 30, 2011 20:19
dea74 escreveu:ivanfx escreveu:Que tal pensarem em primeiro determinar a área do setor e depois determinar a área do triângulo retângulo que é formado traçando um segmento de C1 até C2 ai fica mais fácil para definir a fórmula
Oi Ivan
Só nao consegui enxergar o triangulo. Poderia ser mais explicito?
Abs
Déa
Se riscar um segmento do ponto A até o ponto B você obterá 2 triângulos retângulos, você terá triângulo AC2M e BC2M, basta calcular a área de 1 e depois multiplicar por 2
-
ivanfx
- Usuário Dedicado

-
- Mensagens: 43
- Registrado em: Dom Out 16, 2011 00:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
 por Rosana Vieira » Qua Nov 30, 2011 21:18
por Rosana Vieira » Qua Nov 30, 2011 21:18
ivanfx escreveu:Que tal pensarem em primeiro determinar a área do setor e depois determinar a área do triângulo retângulo que é formado traçando um segmento de C1 até C2 ai fica mais fácil para definir a fórmula
Ivan na atividade 2a é esta fórmula A= R2 (? – sem ?)
Ainda não estou entendendo o exercício
-
Rosana Vieira
- Usuário Parceiro

-
- Mensagens: 74
- Registrado em: Qui Nov 17, 2011 00:11
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por ivanfx » Qua Nov 30, 2011 21:49
por ivanfx » Qua Nov 30, 2011 21:49
orientação dada pelo tutor agora pouco
1) A área da intersecção das duas circunferências (círculos) pode ser calculada como 2 vezes a área do segmento circular de uma delas. Esse segmento circular, por sua vez, pode ser calculado como sendo a área do setor circular menos a área do triângulo isósceles. Agora, para encontrar a área desse triângulo, você deve descobrir o valor de AB. Como? Faça um Teorema de Pitágoras com AB/2 sendo um dos catetos, s o outro cateto e R, a hipotenusa. A sua resposta deve ficar em função dos dados do enunciado.
2) Há outra maneira de se resolver o problema: o procedimento é o mesmo descrito acima. A única mudança é no cálculo da área do triângulo. Observe que se você sabe o raio e o ângulo, então a área desse triângulo é dada por (R.R.sen(teta))/2. Nesse caso, a resposta ficará em função de apenas duas variáveis: R e "teta".
Ambas as resoluções são absolutamente corretas. O único problema é que os itens b e c atribui valores para s. Sendo assim, é fundamental que você saiba a fórmula em função das três variáveis: R, "teta" e s, que é a primeira maneira. No item b, as circunferências serão tangentes externamente e a área da intersecção será igual a ... No item c, as circunferências estarão sobrepostas e a área da intersecção será igual a
-
ivanfx
- Usuário Dedicado

-
- Mensagens: 43
- Registrado em: Dom Out 16, 2011 00:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
 por dea74 » Qua Nov 30, 2011 22:00
por dea74 » Qua Nov 30, 2011 22:00
ivanfx escreveu:orientação dada pelo tutor agora pouco
1) A área da intersecção das duas circunferências (círculos) pode ser calculada como 2 vezes a área do segmento circular de uma delas. Esse segmento circular, por sua vez, pode ser calculado como sendo a área do setor circular menos a área do triângulo isósceles. Agora, para encontrar a área desse triângulo, você deve descobrir o valor de AB. Como? Faça um Teorema de Pitágoras com AB/2 sendo um dos catetos, s o outro cateto e R, a hipotenusa. A sua resposta deve ficar em função dos dados do enunciado.
2) Há outra maneira de se resolver o problema: o procedimento é o mesmo descrito acima. A única mudança é no cálculo da área do triângulo. Observe que se você sabe o raio e o ângulo, então a área desse triângulo é dada por (R.R.sen(teta))/2. Nesse caso, a resposta ficará em função de apenas duas variáveis: R e "teta".
Ambas as resoluções são absolutamente corretas. O único problema é que os itens b e c atribui valores para s. Sendo assim, é fundamental que você saiba a fórmula em função das três variáveis: R, "teta" e s, que é a primeira maneira. No item b, as circunferências serão tangentes externamente e a área da intersecção será igual a ... No item c, as circunferências estarão sobrepostas e a área da intersecção será igual a
Valeu Ivan, agora entendi
-
dea74
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qua Nov 30, 2011 19:22
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Licenciatura em matemática
- Andamento: formado
 por Francesca Vilanni » Qua Nov 30, 2011 22:11
por Francesca Vilanni » Qua Nov 30, 2011 22:11
Se vc não usar o s na fórmula, basta justificar, dizendo que s varia de forma inversamente proporcional a teta.
-
Francesca Vilanni
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Sáb Out 22, 2011 22:31
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por vanessa_mat » Qua Nov 30, 2011 22:29
por vanessa_mat » Qua Nov 30, 2011 22:29
Rosana Vieira escreveu:vanessa_mat escreveu:Considere duas circunferências de raios iguais a R e centro em C1 e C2 , conforme a figura abaixo. Sabendo que a distância entre C1 e C2 é dada por 2s ( 0?s?R ) e que o ângulo A(C_2 ) ?B=?,
Considere duas circunferências de raios iguais a R e centro em C1 e C2 , conforme a figura abaixo. Sabendo que a distância entre C1 e C2 é dada por 2s ( 0?s?R ) e que o ângulo A(C_2 ) ?B=?,
a) Obtenha a expressão que fornece a área superposta
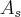
das duas circunferência em função de R,s e

A letra a, depois de muitas tentativas e por enquanto uma noite sem dormir fiz achando a área do setor circular menos a área do triangulo, esse resultado vezes dois:: ficou uma sopa de letrinhas, mas a intenção era essa!!! agora não estou conseguindo resolver o item b e c . Será que alguém pode me dar uma ajudinha???? Já teho a expressão do item a, mas não entendi como proceder nos itens seguintes!!!
b)Qual a posição relativa das circunferências quando A_s=0? Justifique utilizando a expressão obtida em a).
c)Qual a posição relativa das circunferências quando A_s=?R^2? Justifique utilizando a expressão obtida em a).
Vanessa na atividade 2a é esta fórmula A= R2 (? – sem ?)[/quote]
área do setor circular:
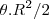
área do tri : Rs-s^2
2.(área do setor circular- área do tri)? a minha deu diferente da sua!!! porque será??
-
vanessa_mat
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Seg Nov 21, 2011 16:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por vanessa_mat » Qua Nov 30, 2011 22:39
por vanessa_mat » Qua Nov 30, 2011 22:39
ivanfx escreveu:orientação dada pelo tutor agora pouco
1) A área da intersecção das duas circunferências (círculos) pode ser calculada como 2 vezes a área do segmento circular de uma delas. Esse segmento circular, por sua vez, pode ser calculado como sendo a área do setor circular menos a área do triângulo isósceles. Agora, para encontrar a área desse triângulo, você deve descobrir o valor de AB. Como? Faça um Teorema de Pitágoras com AB/2 sendo um dos catetos, s o outro cateto e R, a hipotenusa. A sua resposta deve ficar em função dos dados do enunciado.
2) Há outra maneira de se resolver o problema: o procedimento é o mesmo descrito acima. A única mudança é no cálculo da área do triângulo. Observe que se você sabe o raio e o ângulo, então a área desse triângulo é dada por (R.R.sen(teta))/2. Nesse caso, a resposta ficará em função de apenas duas variáveis: R e "teta".
Ambas as resoluções são absolutamente corretas. O único problema é que os itens b e c atribui valores para s. Sendo assim, é fundamental que você saiba a fórmula em função das três variáveis: R, "teta" e s, que é a primeira maneira. No item b, as circunferências serão tangentes externamente e a área da intersecção será igual a ... No item c, as circunferências estarão sobrepostas e a área da intersecção será igual a
Não consegui entender ainda o item b e c, o item a tinha feito igual ao seu comentário que tb tinha recebido uma orientação parecida, a única diferença foi que na área do setor circular fiz: área do círculo é diretamente proporcional a do ângulo central A=

e a área do triângulo Rs - s^2. Será :
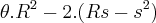
.
Vc pode me ajudar a continuar???
-
vanessa_mat
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Seg Nov 21, 2011 16:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
Voltar para Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
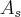 das duas circunferência em função de R,s e
das duas circunferência em função de R,s e


 (
(


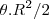
 e a área do triângulo Rs - s^2. Será :
e a área do triângulo Rs - s^2. Será : 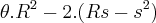 .
.




