Olá
Sergio.
O adjetivo que você usou não cabe a mim, de qualquer forma vou fazer alguns comentários.
Sobre as suas duas perguntas, apenas formalizando, em outras palavras, de fato você quer resolução para os seguintes problemas:
1) Sendo
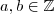
, prove que:

Neste caso,

e

estão limitados ao conjunto dos inteiros, mas a idéia pode ser extendida para outros conjuntos.
2) Sendo

, prove que:
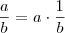
Embora a
teoria dos conjuntos esteja presente em praticamente todos as aspectos matemáticos, este tema é mais tratado em
álgebra.
Farei um breve percurso teórico nestas provas que, matematicamente, responderá as suas perguntas.
Mas, a abstração e uma didática interpretação destes resultados, sim, continuará sendo um desafio.
E mesmo citando o curso de graduação da USP, acredite, salvo algumas raras exceções, para nossa decepção, os professores passam longe deste trabalho.
Lidar com as sutilezas, fica por conta do aluno.
Assuntos como estes são tratados como triviais no ensino pré-graduação, uma vez que requerem uma pesada carga teórica, com um grau de formalização até então não utilizado.
Sobre parte desta teoria, veja em nossa bibliografia, você encontrará assuntos relacionados em:
MILIES, Francisco César Polcino e COELHO, Sônia Pitta. Números: Uma Introdução à Matemática, 3a.edição. São Paulo: EDUSP, 2003.
Recomendo a leitura da introdução.
Sendo mais específico, da página 13 à 18, você terá conteúdo sobre sua dúvida 1.
E da página 156 à 163, sobre a sua dúvida 2.
Você verá que para começar, é necessária uma introdução axiomática.
Pesquise também sobre
anéis, domínios de integridade e corpos, veja em:
GONÇALVES, Adilson. Introdução à álgebra, 5a.edição. Rio de Janeiro: IMPA, 2006.
O conjunto dos inteiros é um
domínio de integridade.
O conjunto dos racionais é um
corpo.
No caso
(1), como

é um
domínio de integridade, este conjunto satisfaz um grupo de axiomas relacionados às operações de soma e produto: propriedade associativa da soma, existência do elemento neutro aditivo, existência do oposto aditivo, comutatividade da soma, associatividade do produto, distributividade à esquerda e à direita, é um anel com unidade, comutativo e não tem divisores de zero.
Para provarmos (1), partimos do axioma do oposto aditivo:
Existência do oposto: para cada inteiro

existe um único elemento que chamaremos oposto de

e indicaremos por

, tal que
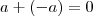
Este axioma também pode ser interpretado assim:
O oposto de um elemento

é o único inteiro que verifica a equação

.
Então, precisamos antes provar (i):
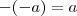
Observando que

verifica a equação

.
Conseqüentemente,

é o oposto de

que é o elemento indicado por

Na seqüência, precisamos provar (ii):
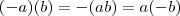
Para a primeira igualdade, observamos que
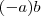
é a solução de

, já que:
![ab+(-a)b=[(-a)+a]b=0 \cdot b = 0 ab+(-a)b=[(-a)+a]b=0 \cdot b = 0](/latexrender/pictures/db115fa80324be92847383b15992d001.png)
Da mesma forma,
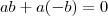
.
E finalmente, para (1), aplicamos (ii):

E usando (i) no último termo, segue que:

.
Sergio, repare que este é um resumo do formalismo e que muitos conceitos aqui citados podem ser bem explorados, como por exemplo, provar que o conjunto dos inteiros é, de fato, um domínio de integridade.
Além do que, não citei explicitamente os axiomas, apenas fiz referência aos nomes.
Para provarmos
(2), partimos da seguinte definição de produto entre elementos racionais:
Sejam

e

elementos de

.
O
produto de

por

será o racional

obtido da seguinte forma:

Sendo
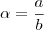
e

.
Então, é necessário verificar que esta definição independe dos representantes, da seguinte forma, provando este lema:
Lema: Sejam

e

números racionais. Então,

Prova do lema: da hipótese, escrevemos:


Daqui, multiplicamos membro a membro:

Reescrevemos (propriedade associativa do produto):

E finalmente,

Ou seja, este lema nos diz que a defnição de produto vale para qualquer elemento racional.
Então, para provar (2), vamos partir do segundo membro:
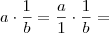
Aplicação da definição de produto:
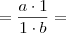
Agora vamos aplicar o axioma da existência da unidade, lembrando que podemos fazer isso pois

é domínio de integridade:

Note que os argumentos matemáticos necessários para esclarecer suas perguntas, precisam passar por este formalismo resumido aqui.
A leitura complementar é fundamental.
Espero não ter piorado.
Um abraço!



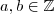 , prove que:
, prove que: 
e
estão limitados ao conjunto dos inteiros, mas a idéia pode ser extendida para outros conjuntos.
 , prove que:
, prove que: 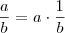
 é um domínio de integridade, este conjunto satisfaz um grupo de axiomas relacionados às operações de soma e produto: propriedade associativa da soma, existência do elemento neutro aditivo, existência do oposto aditivo, comutatividade da soma, associatividade do produto, distributividade à esquerda e à direita, é um anel com unidade, comutativo e não tem divisores de zero.
é um domínio de integridade, este conjunto satisfaz um grupo de axiomas relacionados às operações de soma e produto: propriedade associativa da soma, existência do elemento neutro aditivo, existência do oposto aditivo, comutatividade da soma, associatividade do produto, distributividade à esquerda e à direita, é um anel com unidade, comutativo e não tem divisores de zero. existe um único elemento que chamaremos oposto de
existe um único elemento que chamaremos oposto de  e indicaremos por
e indicaremos por  , tal que
, tal que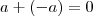
 é o único inteiro que verifica a equação
é o único inteiro que verifica a equação  .
.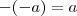
 verifica a equação
verifica a equação  .
. é o oposto de
é o oposto de  que é o elemento indicado por
que é o elemento indicado por 
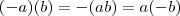
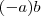 é a solução de
é a solução de  , já que:
, já que:![ab+(-a)b=[(-a)+a]b=0 \cdot b = 0 ab+(-a)b=[(-a)+a]b=0 \cdot b = 0](/latexrender/pictures/db115fa80324be92847383b15992d001.png)
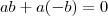 .
.
 .
. e
e  elementos de
elementos de  .
. por
por  será o racional
será o racional  obtido da seguinte forma:
obtido da seguinte forma:
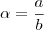 e
e  .
. e
e  números racionais. Então,
números racionais. Então,





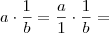
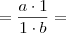
é domínio de integridade:



 .
.
 :
: