integração e a fórmula
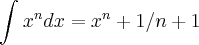 + k, sendo k
+ k, sendo kconstante.
![\int_{}^{} x + 1/\sqrt[4]{}x^5 \int_{}^{} x + 1/\sqrt[4]{}x^5](/latexrender/pictures/2e1587d3c77eca9c2582781f3df71f16.png)
Consegui termina não sei se está certo-
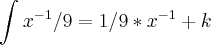
Obrigada pela ajuda!!


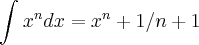 + k, sendo k
+ k, sendo k![\int_{}^{} x + 1/\sqrt[4]{}x^5 \int_{}^{} x + 1/\sqrt[4]{}x^5](/latexrender/pictures/2e1587d3c77eca9c2582781f3df71f16.png)
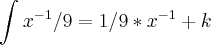


Fernandadb escreveu:Não sei resolver está questão, Calcule as integrais usando os principais teoremas de
integração e a fórmula, sendo k
constante.
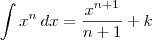
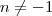 .
.![\int x + \frac{1}{\sqrt[4]{x^5}} \,dx \int x + \frac{1}{\sqrt[4]{x^5}} \,dx](/latexrender/pictures/dbe3a82f65f49df4b88f52506bb1998d.png)
![\int x + \frac{1}{\sqrt[4]{x^5}} \,dx = \int x \,dx + \int x^{-\frac{5}{4}} \,dx \int x + \frac{1}{\sqrt[4]{x^5}} \,dx = \int x \,dx + \int x^{-\frac{5}{4}} \,dx](/latexrender/pictures/79aafb026bd970028ad7fc361c73f34c.png)
![\int \frac{x+1}{\sqrt[4]{x^5}} \,dx \int \frac{x+1}{\sqrt[4]{x^5}} \,dx](/latexrender/pictures/e3d00853756908689b42f2cf9bbc7082.png)
![\int \frac{x+1}{\sqrt[4]{x^5}} \,dx = \int \frac{x}{\sqrt[4]{x^5}} \,dx + \int \frac{1}{\sqrt[4]{x^5}} \,dx \int \frac{x+1}{\sqrt[4]{x^5}} \,dx = \int \frac{x}{\sqrt[4]{x^5}} \,dx + \int \frac{1}{\sqrt[4]{x^5}} \,dx](/latexrender/pictures/1dda602b73dedd72935bbf371fa156d6.png)
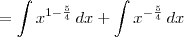
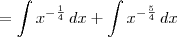

Fernandadb escreveu:
Consegui termina não sei se está certo-
Obrigada pela ajuda!!
![\int x + \frac{1}{\sqrt[4]{x^5}} \,dx \int x + \frac{1}{\sqrt[4]{x^5}} \,dx](/latexrender/pictures/dbe3a82f65f49df4b88f52506bb1998d.png) , temos que:
, temos que:![\int x + \frac{1}{\sqrt[4]{x^5}} \,dx = \int x \,dx + \int x^{-\frac{5}{4}} \,dx \int x + \frac{1}{\sqrt[4]{x^5}} \,dx = \int x \,dx + \int x^{-\frac{5}{4}} \,dx](/latexrender/pictures/79aafb026bd970028ad7fc361c73f34c.png)
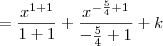
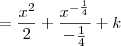
![= \frac{x^2}{2} - \frac{4}{\sqrt[4]{x}} + k = \frac{x^2}{2} - \frac{4}{\sqrt[4]{x}} + k](/latexrender/pictures/7644e24a3a0299878dabde9b4191d539.png)
![\int \frac{x+1}{\sqrt[4]{x^5}} \,dx \int \frac{x+1}{\sqrt[4]{x^5}} \,dx](/latexrender/pictures/e3d00853756908689b42f2cf9bbc7082.png) , temos que:
, temos que:![\int \frac{x+1}{\sqrt[4]{x^5}} \,dx = \int x^{-\frac{1}{4}} \, dx + \int x^{-\frac{5}{4}} \,dx \int \frac{x+1}{\sqrt[4]{x^5}} \,dx = \int x^{-\frac{1}{4}} \, dx + \int x^{-\frac{5}{4}} \,dx](/latexrender/pictures/b14366304418b10d016e47a7f6cb7287.png)
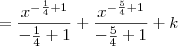
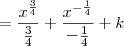
![= \frac{4}{3}\sqrt[4]{x^3} - \frac{4}{\sqrt[4]{x}} + k = \frac{4}{3}\sqrt[4]{x^3} - \frac{4}{\sqrt[4]{x}} + k](/latexrender/pictures/33b91253e6675aaf9ffd035ff3c7e927.png)

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes

 .
.



