 por joaofonseca » Seg Nov 28, 2011 00:38
por joaofonseca » Seg Nov 28, 2011 00:38
Dada a função
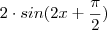
encontrei os dados para desenhar o grafico.
AmplitudeÉ o valor absoluto do fator que multiplica o seno. Ou seja, 2. Quer dizer que o contradomidio será
![[-2,2] [-2,2]](/latexrender/pictures/98fab4cc523eb62bb9cf3a4fbefb7a69.png)
.
PeriodoO periodo da função elementar
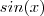
é
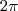
, mas como a variavel independente multiplica por 2.Então o periodo desta função será

.
Ãngulo de desfasamento O valor do desfasamento será

Tudo bem,até agora!Mas o livro de exercicios pergunta quais os pontos de interseção com a função
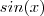
no intervalo de
![[0,2\pi] [0,2\pi]](/latexrender/pictures/1cc5fb6d3b10cf0b4029e23d46fa7fc0.png)
.
Ou seja pede para resolver a equação
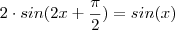
.
Eu não sei por onde começar, pois os ãngulos não são iguais.De um lado temos
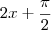
do outro

.
Alguém me ajuda?Obrigado
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por TheoFerraz » Seg Nov 28, 2011 14:26
por TheoFerraz » Seg Nov 28, 2011 14:26
queremos então resolver a seguinte
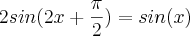
duas coisas podemos fazer, vamos pela mais obvia... Expanda o termo da esquerda como uma soma de arcos, lembrando que
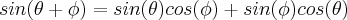
otimo, já da pra tentar né ?
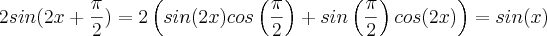
o mais lindo de tudo é que pi/2 vai zerar algumas coisas e vai fazer virar 1 outras... dai voce tem algo bem simples.
caso necessario use :
![sin( \alpha) = \pm \;\; \sqrt[]{1- {cos}^{2}(\alpha)} sin( \alpha) = \pm \;\; \sqrt[]{1- {cos}^{2}(\alpha)}](/latexrender/pictures/873d5571de6a61dc1e4f2e7e4da7f783.png)
divirta-se
-
TheoFerraz
- Colaborador Voluntário

-
- Mensagens: 107
- Registrado em: Qua Abr 13, 2011 19:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Física
- Andamento: cursando
 por joaofonseca » Seg Nov 28, 2011 20:23
por joaofonseca » Seg Nov 28, 2011 20:23
Obrigado pela ajuda.
Depois de aplicar a formula da soma eu cheguei ao seguinte:
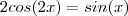
Depois apliquei a formula do ângulo duplo e assim obtive uma expressão quadratica:
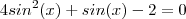
Como aparentemente esta expressão não é fatorável.Apliquei a formula de bhaskara.Obtive:
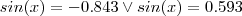
Apliquei a inversa do seno e obtive (radianos):
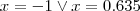
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por TheoFerraz » Seg Nov 28, 2011 21:43
por TheoFerraz » Seg Nov 28, 2011 21:43
joaofonseca escreveu:Como aparentemente esta expressão não é fatorável.Apliquei a formula de bhaskara.Obtive:
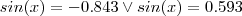
Apliquei a inversa do seno e obtive (radianos):
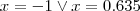
Bem legal isso que voce fez! Eu não usaria isso! foi bem legal!
mas tome um cuidado!
ao aplicar a função inversa em um sin(x) = B
voce precisa obter duas respostas!
Existem sempre dois angulos x que tem um seno específico....
Voce sabe como achar o outro tendo um! Transponha os quadrantes!
um angulo no primeiro quadrante terá um seno igual à sua equivalencia no segundo quadrante!
e um angulo no terceiro quadrante terá um seno igual à sua equivalencia no quarto quadrante!
está acompanhando? sinto que estou sendo levemente negligente, mas vi que voce tem raciocínio rápido!
seu resultado está correto porém incompleto... existem mais 2 respostas

Uploaded with
ImageShack.usATENÇÂO: Por mais que a figura esteja mostrando 5 pontos, perceba que o primeiro e o ultimo são o mesmo...
-
TheoFerraz
- Colaborador Voluntário

-
- Mensagens: 107
- Registrado em: Qua Abr 13, 2011 19:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Física
- Andamento: cursando
 por joaofonseca » Seg Nov 28, 2011 23:29
por joaofonseca » Seg Nov 28, 2011 23:29
As soluções dizem respeito aos angulos de referência.Sendo o seno uma função periodica, existirão infinitas soluções.
Mas para efeitos académicos, decidi fazer uma pequena alteração à expressão anterior.Em vez de ter amplitude 2, terá amplitude 1 e por isso fica assim:
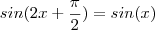
Aplicando sucessivamente a identidade da soma e do duplo angulo, fica:
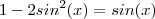
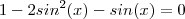
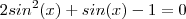
Como se pode verificar, já se pode fatorar com facilidade.
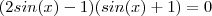
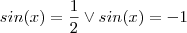
Estes valores já nos fazem lembrar dos angulos notaveis (aqueles angulos para os quais devemos saber os valores)
Assim:
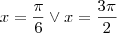
Estas são as soluções no intervalo
![[0,2\pi] [0,2\pi]](/latexrender/pictures/1cc5fb6d3b10cf0b4029e23d46fa7fc0.png)
.Se quisermos saber todas as soluções escrevemos:
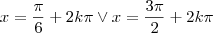
em que k pertence aos numeros inteiros.
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por TheoFerraz » Ter Nov 29, 2011 15:53
por TheoFerraz » Ter Nov 29, 2011 15:53
Na função que foi dada no enunciado existem 4 pontos de interssecção. na função que voce resolveu usar na ultima resposta, de fato existem apenas 2.
-
TheoFerraz
- Colaborador Voluntário

-
- Mensagens: 107
- Registrado em: Qua Abr 13, 2011 19:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Física
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Equação trigonométrica] Resolução da equação
por JessicaAraujo » Qui Abr 11, 2013 15:59
- 2 Respostas
- 1729 Exibições
- Última mensagem por JessicaAraujo

Qui Abr 11, 2013 19:12
Funções
-
- Equação Trigonométrica.
por rodsales » Sáb Ago 29, 2009 18:41
- 4 Respostas
- 4047 Exibições
- Última mensagem por rodsales

Sáb Ago 29, 2009 21:19
Trigonometria
-
- equação trigonométrica
por thaa_121 » Qui Abr 08, 2010 15:22
- 1 Respostas
- 3786 Exibições
- Última mensagem por Molina

Qui Abr 08, 2010 23:58
Trigonometria
-
- [Equação Trigonométrica]Equação trigonométrica
por gustavoluiss » Ter Ago 09, 2011 00:32
- 12 Respostas
- 8224 Exibições
- Última mensagem por gustavoluiss

Qua Ago 10, 2011 18:20
Trigonometria
-
- Equação trigonométrica?
por Malorientado » Qua Ago 22, 2012 23:55
- 3 Respostas
- 1653 Exibições
- Última mensagem por Russman

Qui Ago 23, 2012 22:03
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
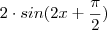 encontrei os dados para desenhar o grafico.
encontrei os dados para desenhar o grafico.![[-2,2] [-2,2]](/latexrender/pictures/98fab4cc523eb62bb9cf3a4fbefb7a69.png) .
.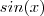 é
é 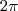 , mas como a variavel independente multiplica por 2.Então o periodo desta função será
, mas como a variavel independente multiplica por 2.Então o periodo desta função será  .
.
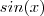 no intervalo de
no intervalo de ![[0,2\pi] [0,2\pi]](/latexrender/pictures/1cc5fb6d3b10cf0b4029e23d46fa7fc0.png) .
.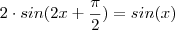 .
.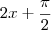 do outro
do outro  .
.

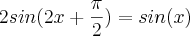
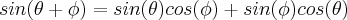
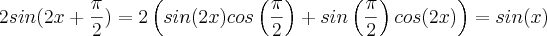
![sin( \alpha) = \pm \;\; \sqrt[]{1- {cos}^{2}(\alpha)} sin( \alpha) = \pm \;\; \sqrt[]{1- {cos}^{2}(\alpha)}](/latexrender/pictures/873d5571de6a61dc1e4f2e7e4da7f783.png)
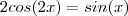
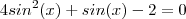
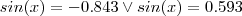
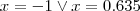

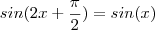
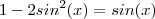
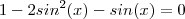
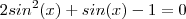
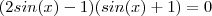
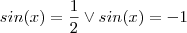
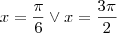
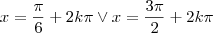 em que k pertence aos numeros inteiros.
em que k pertence aos numeros inteiros.




