 por beel » Dom Nov 27, 2011 20:44
por beel » Dom Nov 27, 2011 20:44
Qual o volume de um solido gerado pela rotação em torno do eixo Ox , sendo que sua função é f(x) =

, com x E [0,1].
Eu fiz assim:
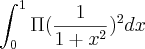
,
mas fiquei em duvida na substituiçao.Coloquei u=a.tg(theta)
mas ai x²=tg(theta)
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por LuizAquino » Seg Nov 28, 2011 16:32
por LuizAquino » Seg Nov 28, 2011 16:32
beel escreveu:Eu fiz assim:
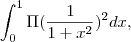
mas fiquei em duvida na substituiçao.Coloquei u=a.tg(theta)
mas ai x²=tg(theta)
Para conferir a resolução da integral, siga os procedimentos abaixo.
- Acesse a página: http://www.wolframalpha.com/
- No campo de entrada, digite:
- Código: Selecionar todos
integrate pi(1/(1 + x^2))^2 dx
- Clique no botão de igual ao lado do campo de entrada.
- Após a integral ser calculada, clique no botão "Show steps" ao lado do resultado.
- Pronto! Agora basta estudar a resolução e comparar com a sua.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por beel » Seg Nov 28, 2011 16:37
por beel » Seg Nov 28, 2011 16:37
Nao aparece a resolução, com substituiçao e etc nesse site...isso nao ajuda muito, mas obg de qualquer forma, de novo.
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por LuizAquino » Seg Nov 28, 2011 17:04
por LuizAquino » Seg Nov 28, 2011 17:04
beel escreveu:Nao aparece a resolução, com substituiçao e etc nesse site...isso nao ajuda muito, mas obg de qualquer forma, de novo.
"Não ajuda muito"?!
Vejamos como usar o procedimento. Através dele, podemos obter o texto abaixo.
Possible intermediate steps:

Factor out constants:
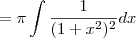
For the integrand, 1/(x^2+1)^2 substitute x = tan(u) and dx = sec^2(u) du. Then (x^2+1)^2 = (tan^2(u)+1)^2 = sec^4(u) and u = tan^(-1)(x):
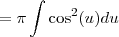
Write cos^2(u) as 1/2 cos(2 u)+1/2:
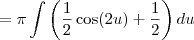
Integrate the sum term by term and factor out constants:

For the integrand cos(2 u), substitute s = 2 u and ds = 2 du:

The integral of cos(s) is sin(s):

The integral of 1/2 is u/2:
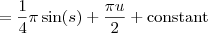
Substitute back for s = 2 u:
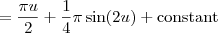
Substitute back for u = tan^(-1)(x):
![= \frac{\pi \left[\left(x^2+1\right) \tan^{-1}(x)+x\right]}{2 \left(x^2+1\right)}+\textrm{constant} = \frac{\pi \left[\left(x^2+1\right) \tan^{-1}(x)+x\right]}{2 \left(x^2+1\right)}+\textrm{constant}](/latexrender/pictures/8a7a86d0bf9a35b4d42df5d8b0812d95.png)
Which is equal to:

Agora tudo que
você precisa fazer é aplicar o Teorema Fundamental do Cálculo:
![\int_{0}^{1}\pi \left(\frac{1}{1+x^2}\right)^2 dx = \left[\frac{1}{2} \pi \left(\frac{x}{x^2+1} + \tan^{-1}(x)\right)\right]_0^1 \int_{0}^{1}\pi \left(\frac{1}{1+x^2}\right)^2 dx = \left[\frac{1}{2} \pi \left(\frac{x}{x^2+1} + \tan^{-1}(x)\right)\right]_0^1](/latexrender/pictures/c28212f6018e3211568250d93d38447f.png)
![= \left[\frac{1}{2} \pi \left(\frac{1}{1^2+1} + \tan^{-1}(1)\right)\right] - \left[\frac{1}{2} \pi \left(\frac{0}{0^2+1} + \tan^{-1}(0)\right)\right] = \left[\frac{1}{2} \pi \left(\frac{1}{1^2+1} + \tan^{-1}(1)\right)\right] - \left[\frac{1}{2} \pi \left(\frac{0}{0^2+1} + \tan^{-1}(0)\right)\right]](/latexrender/pictures/960299fde9f209a9869f11011b908a65.png)
![= \left[\frac{1}{2} \pi \left(\frac{1}{2} + \frac{\pi}{4}\right)\right] - \left[\frac{1}{2} \pi \left(0 + 0\right)\right] = \left[\frac{1}{2} \pi \left(\frac{1}{2} + \frac{\pi}{4}\right)\right] - \left[\frac{1}{2} \pi \left(0 + 0\right)\right]](/latexrender/pictures/bbcc58ab988cfb08da84e037f933782a.png)
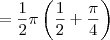
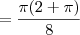
Por fim, você pode conferir o seu resultado digitando no campo de entrada da página indicada:
- Código: Selecionar todos
integrate pi(1/(1 + x^2))^2 dx x=0..1
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por beel » Dom Dez 04, 2011 21:04
por beel » Dom Dez 04, 2011 21:04
Mas na hora de determinar o "u" pra fazer a substituiçao trigonometrica, nao seria x²? foi isso que me confundiu, e foi essa minha duvida...na resolução ele coloca o x como u
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por LuizAquino » Seg Dez 05, 2011 10:30
por LuizAquino » Seg Dez 05, 2011 10:30
beel escreveu:Mas na hora de determinar o "u" pra fazer a substituiçao trigonometrica, nao seria x²? foi isso que me confundiu, e foi essa minha duvida...na resolução ele coloca o x como u
Não. A substituição deve ser como foi indicado na resolução:
(...)
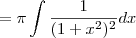
For the integrand, 1/(x^2+1)^2 substitute x = tan(u) and dx = sec^2(u) du.
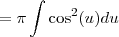
(...)
Fazendo essa substituição, temos que:
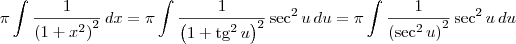

-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [calculo] volume por integral 2
por beel » Dom Nov 27, 2011 20:54
- 3 Respostas
- 3357 Exibições
- Última mensagem por LuizAquino

Seg Dez 05, 2011 11:02
Cálculo: Limites, Derivadas e Integrais
-
- Calculo de volume por Integral definida
 por teteffs » Qui Out 06, 2011 17:32
por teteffs » Qui Out 06, 2011 17:32
- 7 Respostas
- 6714 Exibições
- Última mensagem por teteffs

Sáb Out 08, 2011 20:18
Cálculo: Limites, Derivadas e Integrais
-
- calculo area e volume - integral
por bicio29 » Qui Out 20, 2011 08:41
- 3 Respostas
- 4049 Exibições
- Última mensagem por LuizAquino

Qui Out 20, 2011 10:30
Cálculo: Limites, Derivadas e Integrais
-
- Calculo de volume atravé de integral dupla
 por maiquel » Qua Out 13, 2010 12:34
por maiquel » Qua Out 13, 2010 12:34
- 1 Respostas
- 7392 Exibições
- Última mensagem por armando

Sex Jan 06, 2017 04:14
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo do Volume] Variação do volume em porcentagem
por Douglaasag » Sex Out 10, 2014 09:23
- 0 Respostas
- 4479 Exibições
- Última mensagem por Douglaasag

Sex Out 10, 2014 09:23
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 , com x E [0,1].
, com x E [0,1]. ,
,
 , com x E [0,1].
, com x E [0,1]. ,
,


![\int_{0}^{1}\pi \left(\frac{1}{1+x^2}\right)^2 dx = \left[\frac{1}{2} \pi \left(\frac{x}{x^2+1} + \tan^{-1}(x)\right)\right]_0^1 \int_{0}^{1}\pi \left(\frac{1}{1+x^2}\right)^2 dx = \left[\frac{1}{2} \pi \left(\frac{x}{x^2+1} + \tan^{-1}(x)\right)\right]_0^1](/latexrender/pictures/c28212f6018e3211568250d93d38447f.png)
![= \left[\frac{1}{2} \pi \left(\frac{1}{1^2+1} + \tan^{-1}(1)\right)\right] - \left[\frac{1}{2} \pi \left(\frac{0}{0^2+1} + \tan^{-1}(0)\right)\right] = \left[\frac{1}{2} \pi \left(\frac{1}{1^2+1} + \tan^{-1}(1)\right)\right] - \left[\frac{1}{2} \pi \left(\frac{0}{0^2+1} + \tan^{-1}(0)\right)\right]](/latexrender/pictures/960299fde9f209a9869f11011b908a65.png)
![= \left[\frac{1}{2} \pi \left(\frac{1}{2} + \frac{\pi}{4}\right)\right] - \left[\frac{1}{2} \pi \left(0 + 0\right)\right] = \left[\frac{1}{2} \pi \left(\frac{1}{2} + \frac{\pi}{4}\right)\right] - \left[\frac{1}{2} \pi \left(0 + 0\right)\right]](/latexrender/pictures/bbcc58ab988cfb08da84e037f933782a.png)
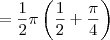
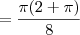


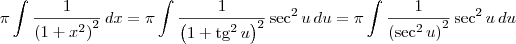


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.