Estou precisando de uma dica sobre como resolver a integral
![\int_{}^{}du / \sqrt[2]{{u}^{2}-{a}^{2}} \int_{}^{}du / \sqrt[2]{{u}^{2}-{a}^{2}}](/latexrender/pictures/09cea9ef7167a1520b8d1520005b1b82.png) . Sei que a resposta é
. Sei que a resposta é ![ln \left|u + \sqrt[2]{{u}^{2}-{a}^{2}} \right|+C ln \left|u + \sqrt[2]{{u}^{2}-{a}^{2}} \right|+C](/latexrender/pictures/f7e2db5047efb97cb206190cc555b136.png) , mas não sei como chegar a essa expressão. Desde já agradeço a atenção dispensada por todos.
, mas não sei como chegar a essa expressão. Desde já agradeço a atenção dispensada por todos.
![\int_{}^{}du / \sqrt[2]{{u}^{2}-{a}^{2}} \int_{}^{}du / \sqrt[2]{{u}^{2}-{a}^{2}}](/latexrender/pictures/09cea9ef7167a1520b8d1520005b1b82.png) . Sei que a resposta é
. Sei que a resposta é ![ln \left|u + \sqrt[2]{{u}^{2}-{a}^{2}} \right|+C ln \left|u + \sqrt[2]{{u}^{2}-{a}^{2}} \right|+C](/latexrender/pictures/f7e2db5047efb97cb206190cc555b136.png) , mas não sei como chegar a essa expressão. Desde já agradeço a atenção dispensada por todos.
, mas não sei como chegar a essa expressão. Desde já agradeço a atenção dispensada por todos.
Cristiano Tavares escreveu:Estou precisando de uma dica sobre como resolver a integral. Sei que a resposta é
, mas não sei como chegar a essa expressão
integrate 1/sqrt(u^2 - a^2) du

![\frac{1}{a}ln\left|u + \sqrt[2]{{u}^{2}-{a}^{2}} \right| \frac{1}{a}ln\left|u + \sqrt[2]{{u}^{2}-{a}^{2}} \right|](/latexrender/pictures/b1f68dd92bff5e7d44d111980c524a0f.png) .
.
Cristiano Tavares escreveu:Na demonstração do site, ao final aparece o logaritmo ln todo dividido por "a", e aí é dito que para valores restritos de "u" e "a", esse "a" pode ser eliminado da expressão, não entendi o porquê disso.
(...)
Which is equivalent for restricted u and a values to:
----------is the natural logarithm.
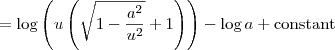
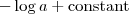 representa uma outra constante real. Vamos chamar essa outra constante de c. Sendo assim, temos que:
representa uma outra constante real. Vamos chamar essa outra constante de c. Sendo assim, temos que: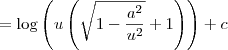
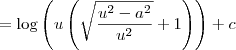

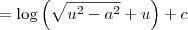
Cristiano Tavares escreveu: Resolvi a integral sozinho e encontrei como resposta.


Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes