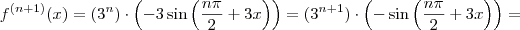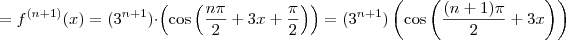por Beatriz4 » Sex Nov 25, 2011 21:25
por Beatriz4 » Sex Nov 25, 2011 21:25
Precisava de ajuda neste exercicio:
Considere a função real de variável real definida por f(x)=cos(3x). Prove pelo método de indução matemática que as sucessivas derivadas de f(x) podem ser dadas pela expressão: f^n'(x)=(3^n)cos(n*pi/2+3x).
Já calculei a primeira derivada, ou seja para n'=1: f'(x)=-3sin(3x) e agora segundo este método tenho de pegar na expressão f^n'(x)=(3^n)cos(n*pi/2+3x) e chegar a f^(n+1)'(x)=(3^(n+1))cos((n+1)*pi/2+3x) ou então vice-versa. Como hei de fazer? Se alguém me puder dar umas luzes agradecia

-
Beatriz4
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sex Nov 25, 2011 21:17
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Biomédica
- Andamento: cursando
 por MarceloFantini » Sex Nov 25, 2011 23:09
por MarceloFantini » Sex Nov 25, 2011 23:09
Perceba que a relação
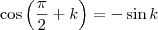
, logo
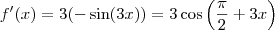
.
Logo, vamos lá: pela hipótese de indução temos que
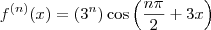
. Derivando, temos:
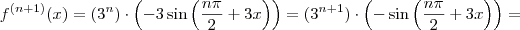
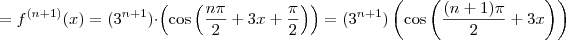
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Beatriz4 » Sex Nov 25, 2011 23:23
por Beatriz4 » Sex Nov 25, 2011 23:23
Obrigada pela rápida resposta e por me teres esclarecido! =)
-
Beatriz4
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sex Nov 25, 2011 21:17
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Biomédica
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Método da indução matématica
 por cardosor23 » Seg Mar 26, 2012 19:38
por cardosor23 » Seg Mar 26, 2012 19:38
- 0 Respostas
- 1116 Exibições
- Última mensagem por cardosor23

Seg Mar 26, 2012 19:38
Álgebra Elementar
-
- Sem utilizar o �método de indução matemática
por Prof Prevaricador » Dom Abr 14, 2013 19:39
- 6 Respostas
- 3564 Exibições
- Última mensagem por e8group

Seg Abr 15, 2013 18:18
Sequências
-
- [Somatório] Provar pelo Método de Indução Matemática
por Prof Prevaricador » Dom Abr 14, 2013 16:25
- 2 Respostas
- 5070 Exibições
- Última mensagem por Prof Prevaricador

Dom Abr 14, 2013 18:35
Sequências
-
- [hipótese da indução] Indução matemática
por leonardoandra » Sáb Out 12, 2013 22:58
- 1 Respostas
- 2683 Exibições
- Última mensagem por leonardoandra

Seg Out 14, 2013 20:10
Equações
-
- Indução Matemática
por gramata » Qua Set 02, 2009 16:52
- 0 Respostas
- 3065 Exibições
- Última mensagem por gramata

Qua Set 02, 2009 16:52
Problemas do Cotidiano
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



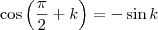 , logo
, logo 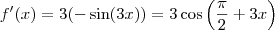 .
.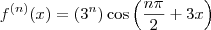 . Derivando, temos:
. Derivando, temos: