Sub-seção para materiais das disciplinas relacionadas à Geometria.
Utilize a área de pedidos para outros ou caso a sub-seção da disciplina ainda não possua material.
Provas aplicadas, notas de aulas, listas de exercícios, gabaritos, bibliografias etc.
Regras do fórum
O objetivo desta seção é compartilhar alguns materiais dos próprios alunos do IME-USP, formandos e formados, das disciplinas do curso de Licenciatura em Matemática.
Dentre os materiais, organizados por disciplinas, você encontrará:
Provas aplicadas, notas de aulas, listas de exercícios, gabaritos e bibliografias, além de outros materiais indicados ou fornecidos pelos próprios professores.
A fonte e os créditos do autor devem ser citados sempre que disponíveis.
O intuito deste compartilhamento é favorecer um estudo complementar.
Utilize a seção de pedidos para outros ou caso a sub-seção ainda não possua material.
A pesquisa do fórum facilita a localização de materiais e outros assuntos já publicados.
 por andersontricordiano » Qui Nov 24, 2011 16:30
por andersontricordiano » Qui Nov 24, 2011 16:30
O volume de um prisma hexagonal regular é
![216\sqrt[]{3} 216\sqrt[]{3}](/latexrender/pictures/a4f6ecd37ebdc5f0077e57441f369c4f.png)
cm³ . Se a área lateral desse prisma é
![144\sqrt[]{3} 144\sqrt[]{3}](/latexrender/pictures/6f2ff757ebd7328a8ac2b3c7fe5f6076.png)
cm² , então a altura desse prisma , em cm mede:
Resposta 5
Agradeço muito quem resolver esse exercício
-
andersontricordiano
- Colaborador Voluntário

-
- Mensagens: 192
- Registrado em: Sex Mar 04, 2011 23:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por TheoFerraz » Qui Nov 24, 2011 17:32
por TheoFerraz » Qui Nov 24, 2011 17:32
não é dificil.
Utilizando as formulas de area lateral, e volume, e igualando-as aos valores dados, voce obterá um sistema, observe.
o volume dum cilindro é SEMPRE :
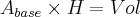
(sendo h a altura)
e a area lateral será bem intuitiva!
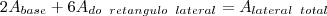
lembrando que a area de um hexagono pode ser vista como a soma de 6 triangulos equiláteros! portanto
![{A}_{hexagono} = 6 \times \frac{{l}^{2}.\sqrt[]{3}}{4} {A}_{hexagono} = 6 \times \frac{{l}^{2}.\sqrt[]{3}}{4}](/latexrender/pictures/571ed2fd04293c8f3737f3ebe94fd145.png)
com isso voce já consegue fazer o exercicio. a base é um hexagono cujo tamanho da arestra é l... esse mesmo l será usado como base dos retangulos da area lateral.
Obs: Visualizando tudo fica mais facil. tente desenhar e dar nome para os lados (SEMPRE)
-
TheoFerraz
- Colaborador Voluntário

-
- Mensagens: 107
- Registrado em: Qua Abr 13, 2011 19:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Física
- Andamento: cursando
Voltar para Geometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (Geometria) Qual a altura do prisma descrito no exercício
por andersontricordiano » Qui Out 06, 2011 13:08
- 0 Respostas
- 2159 Exibições
- Última mensagem por andersontricordiano

Qui Out 06, 2011 13:08
Geometria
-
- Prisma Hexagonal
por Laryssa Rafaella » Sáb Mai 28, 2011 22:04
- 1 Respostas
- 8560 Exibições
- Última mensagem por carlosalesouza

Dom Mai 29, 2011 03:47
Geometria Plana
-
- [Geometria espacial] Prisma hexagonal
por acargo » Dom Out 23, 2011 19:13
- 2 Respostas
- 3059 Exibições
- Última mensagem por acargo

Qui Jan 05, 2012 10:51
Geometria Espacial
-
- Determine a área total e o volume do prisma Hexagonal
por andersontricordiano » Qui Nov 10, 2011 15:55
- 1 Respostas
- 3413 Exibições
- Última mensagem por MarceloFantini

Qui Nov 10, 2011 19:54
Geometria
-
- [Geometria Espacial] Questão sobre Prisma Hexagonal Regular
por passolarg0f » Qui Abr 19, 2012 21:42
- 0 Respostas
- 2626 Exibições
- Última mensagem por passolarg0f

Qui Abr 19, 2012 21:42
Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![216\sqrt[]{3} 216\sqrt[]{3}](/latexrender/pictures/a4f6ecd37ebdc5f0077e57441f369c4f.png) cm³ . Se a área lateral desse prisma é
cm³ . Se a área lateral desse prisma é ![144\sqrt[]{3} 144\sqrt[]{3}](/latexrender/pictures/6f2ff757ebd7328a8ac2b3c7fe5f6076.png) cm² , então a altura desse prisma , em cm mede:
cm² , então a altura desse prisma , em cm mede:
![216\sqrt[]{3} 216\sqrt[]{3}](/latexrender/pictures/a4f6ecd37ebdc5f0077e57441f369c4f.png) cm³ . Se a área lateral desse prisma é
cm³ . Se a área lateral desse prisma é ![144\sqrt[]{3} 144\sqrt[]{3}](/latexrender/pictures/6f2ff757ebd7328a8ac2b3c7fe5f6076.png) cm² , então a altura desse prisma , em cm mede:
cm² , então a altura desse prisma , em cm mede:
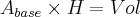
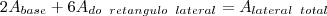
![{A}_{hexagono} = 6 \times \frac{{l}^{2}.\sqrt[]{3}}{4} {A}_{hexagono} = 6 \times \frac{{l}^{2}.\sqrt[]{3}}{4}](/latexrender/pictures/571ed2fd04293c8f3737f3ebe94fd145.png)






