 por Aparecida » Ter Nov 22, 2011 20:55
por Aparecida » Ter Nov 22, 2011 20:55
ivanfx escreveu:Aparecida escreveu:Olá alguém pode me ajudar a começar a resolver esse exercicio
Uma pista oficial de atletismo é composta por 8 raias, cada uma delas com 1,2m de largura, todas são formadas por dois segmentos de reta e duas semicircunferências. O atleta que completar uma volta na raia mais interna percorre exatamente 400m. Assumindo que, durante uma competição, os atletas se mantenham no centro de sua raia, responda o que se pede.
a) Deseja-se construir uma pista na qual cada trecho tenha exatamente 100m de comprimento na raia mais interna . Qual deve ser a medida do raio das semicircunferências que formam o trajeto percorrido por um atleta nessa raia? Explique seu raciocínio e não use aproximações para .
b) Em uma pista oficial, o atleta que completar uma volta pela raia mais externa irá percorrer quanto a mais do que um atleta que completar a volta percorrendo a raia mais interna? Explique seu raciocínio, use e duas ordens decimais quando necessário.
c) Você já deve ter notado que, em algumas competições, os atletas não largam alinhados, mas a linha de chegada é a mesma para todos. Determine a distância entre cada ponto de largada para que todos os atletas, mantendo-se no centro de suas raias, percorram a mesma distância numa corrida de 400m. Explique seu raciocínio e use
Quando for assim abra um novo tópico para não misturar temas, o administrador do site reclama assim:
Vamos lá, para resolver esse problema você imagina uma linha no centro da 1ª raia, observe que o atleta tem que correr no centro da raia.
Também você tem uma semicircunferência, para calcular você utiliza

onde C será 100 metros. Dessa forma irá encontrar o valor do raio.
Para o item b você pensa assim: encontrado o raio da 1º raia você irá encontrar o raio da 8ª raia, basta fazer raio da primeira raia + 7 x 1,2
Após descobrir o raio da da 8ª raia você vai calcular o comprimento da circunferência da 1ª raia

e o comprimento da circunferência da 8ª raia utilizando a mesma fórmula anterior. (Porque calcular o comprimento da circunferência ? Justamente porque a pista possui duas semicircunferências iguais que juntando forma uma circunferência. Após calcular o comprimento da circunferência subtraia um valor do outro e obterá o resultado de que precisa.
o item c posto depois
OLA MUITO OBRIGADA PELA ORIENTAÇÃO, EU FIZ OS CALCULOS NAO ESTAVA CONSIGUINDO ESCREVER COMO ESTA SENDO FEITO OS CALCULOS.
-
Aparecida
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Dom Out 30, 2011 22:22
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica
- Andamento: formado
 por Tata » Ter Nov 22, 2011 21:26
por Tata » Ter Nov 22, 2011 21:26
Oi, alguém poderia enviar a resolução do sistemas de equações diofantina para o meu email também?
prof_online@hotmail.comObrigada!
Tata
-
Tata
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Nov 22, 2011 18:04
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Tata » Ter Nov 22, 2011 21:31
por Tata » Ter Nov 22, 2011 21:31
Oi pode enviar a resolução do sistema de equações diofantina para o meu email tb?
prof_online@hotmail.comObrigada
-
Tata
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Nov 22, 2011 18:04
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Francesca Vilanni » Ter Nov 22, 2011 22:57
por Francesca Vilanni » Ter Nov 22, 2011 22:57
Na questão da D1 foi postado que o comprimento da circunferência era 100, creio que seja 200, pois é 100 para cada parte.
Certo????
-
Francesca Vilanni
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Sáb Out 22, 2011 22:31
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por vanessa_mat » Ter Nov 22, 2011 23:28
por vanessa_mat » Ter Nov 22, 2011 23:28
Estou vendo que vcs estão dispostos a trocar idéias,porém no momento não posso lhes ajudar estou tentando resolver a equação diofantina que nem sei por onde começar e o sistema linear, estava tentando isolar incógnita, até regra de Cramer eu tentei mas não deu certo porque tem duas equações somente, será que alguém pode me auxiliar??agradeço, estou começando agora no grupo de vcs e quero aprender e poder ajudar
vanessa.macastilho@gmail.comEditado pela última vez por
vanessa_mat em Ter Nov 22, 2011 23:33, em um total de 1 vez.
-
vanessa_mat
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Seg Nov 21, 2011 16:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por vanessa_mat » Ter Nov 22, 2011 23:32
por vanessa_mat » Ter Nov 22, 2011 23:32
Rosana Vieira escreveu:Olá alguém pode me ajudar a resolver o seguinte sistema linear
Encontre as soluções inteiras do sistema de equações lineares:
x + Y + z = 100
x + 8y + 50z = 156
Agradeço desde já.
Também já tentei de várias maneiras até cramer tentei,mas só tem duas equações e não dá certo!!!!
help-me
vanessa.macastilho@gmail.com
-
vanessa_mat
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Seg Nov 21, 2011 16:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por ivanfx » Ter Nov 22, 2011 23:40
por ivanfx » Ter Nov 22, 2011 23:40
Francesca Vilanni escreveu:Na questão da D1 foi postado que o comprimento da circunferência era 100, creio que seja 200, pois é 100 para cada parte.
Certo????
O raio pode ser calculado com a semicircunferência, para isso você utilizará

para comprimento da semicircunferência que é 100
Se for utilizar as duas semicircunferências que forma uma circunferência a fórmula é

e ai sim você utiliza para o comprimento da circunferência 200
-
ivanfx
- Usuário Dedicado

-
- Mensagens: 43
- Registrado em: Dom Out 16, 2011 00:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
 por Lourdes » Qua Nov 23, 2011 17:12
por Lourdes » Qua Nov 23, 2011 17:12
Olá, estou com muitas dúvidas na atividade de equação diofantina e sistema de equação linear, por favor gostaria que me auxiliassem, pois venho tentando fazer e não me recordo mais desse conteúdo. obrigada
meu email é:
lourdes.vfreitas@yahoo.com.br
-
Lourdes
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qui Out 27, 2011 23:01
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: formado
 por edsonmota » Qua Nov 23, 2011 22:34
por edsonmota » Qua Nov 23, 2011 22:34
silvia fillet escreveu:Rosana, enviei o seu e-mail que eu passo a resoluçao.
Oi Silvia, tudo bem?
Estava acompanhando o fórum apenas observando, porém gostaria de ajudar e também receber ajuda. Nesse caso estou encontrando dificuldades nesse exercício. Pode enviar para mim também?
Meu email:
edsonmotadossantos@ig.com.brGrato
-
edsonmota
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Ter Nov 22, 2011 21:30
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por Miriam » Qua Nov 23, 2011 22:42
por Miriam » Qua Nov 23, 2011 22:42
Rosana Vieira escreveu:Olá alguém pode me ajudar a resolver o seguinte sistema linear
Encontre as soluções inteiras do sistema de equações lineares:
x + Y + z = 100
x + 8y + 50z = 156
Agradeço desde já.
qdo vc faz a adição das equações (multiplicando uma delas por -1), cai numa equação diofantina. Então, encontre o mdc dos coeficientes e verifique que ele divide o segundo membro. Encontre uma solução particular e em seguida, substitua os valores em uma das equações.
encontrei a seguinte solução: x = 98 -t; y = 1 + 7t; z = 1 - t.
Coincide com a de alguém?
-
Miriam
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Ter Out 25, 2011 20:57
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: formado
 por edsonmota » Qui Nov 24, 2011 00:03
por edsonmota » Qui Nov 24, 2011 00:03
Miriam escreveu:Rosana Vieira escreveu:Olá alguém pode me ajudar a resolver o seguinte sistema linear
Encontre as soluções inteiras do sistema de equações lineares:
x + Y + z = 100
x + 8y + 50z = 156
Agradeço desde já.
qdo vc faz a adição das equações (multiplicando uma delas por -1), cai numa equação diofantina. Então, encontre o mdc dos coeficientes e verifique que ele divide o segundo membro. Encontre uma solução particular e em seguida, substitua os valores em uma das equações.
encontrei a seguinte solução: x = 98 -t; y = 1 + 7t; z = 1 - t.
Coincide com a de alguém?
Oi Miriam,
Não seria x = 98 - 6 t
x + 1 + 7t + 1 - t = 100
x + 2 + 6t = 100
x = 100 - 2 - 6t
x = 98 - 6t
-
edsonmota
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Ter Nov 22, 2011 21:30
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por Miriam » Qui Nov 24, 2011 12:33
por Miriam » Qui Nov 24, 2011 12:33
edsonmota escreveu:Miriam escreveu:Rosana Vieira escreveu:Olá alguém pode me ajudar a resolver o seguinte sistema linear
Encontre as soluções inteiras do sistema de equações lineares:
x + Y + z = 100
x + 8y + 50z = 156
Agradeço desde já.
qdo vc faz a adição das equações (multiplicando uma delas por -1), cai numa equação diofantina. Então, encontre o mdc dos coeficientes e verifique que ele divide o segundo membro. Encontre uma solução particular e em seguida, substitua os valores em uma das equações.
encontrei a seguinte solução: x = 98 -t; y = 1 + 7t; z = 1 - t.
Coincide com a de alguém?
Oi Miriam,
Não seria x = 98 - 6 t
x + 1 + 7t + 1 - t = 100
x + 2 + 6t = 100
x = 100 - 2 - 6t
x = 98 - 6t
Olá Edson...
Tem razão...digitei errado.
Obrigada
-
Miriam
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Ter Out 25, 2011 20:57
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: formado
 por didigica » Qui Nov 24, 2011 17:17
por didigica » Qui Nov 24, 2011 17:17
silvia fillet escreveu:Rosana, enviei o seu e-mail que eu passo a resoluçao.
olá silvia meu e-mail é
andreiabreve@hotmail.com please me ajude
-
didigica
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Seg Nov 07, 2011 20:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura matematica
- Andamento: formado
 por linejak2005 » Qui Nov 24, 2011 20:07
por linejak2005 » Qui Nov 24, 2011 20:07
Olá pessoal estou tentando resolver e as minhas respostas foram:
x= -104- 103t -102u
y= -104 - 103t -101u
z= -1-t
confere com a de alguem????
silvia poderia me enviar um e-mail:
linejak2005@yahoo.com.brObrigada
-
linejak2005
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qua Nov 23, 2011 21:13
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Miriam » Qui Nov 24, 2011 22:51
por Miriam » Qui Nov 24, 2011 22:51
linejak2005 escreveu:Olá pessoal estou tentando resolver e as minhas respostas foram:
x= -104- 103t -102u
y= -104 - 103t -101u
z= -1-t
confere com a de alguem????
silvia poderia me enviar um e-mail:
linejak2005@yahoo.com.brObrigada
Eu encontrei x=104+103t-102k, y=104+103t-101k e z=-1-t
Nossas respostas estão bem parecidas, exceto pelos sinais em x e y. Vou rever.
-
Miriam
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Ter Out 25, 2011 20:57
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: formado
 por deboralino » Sex Nov 25, 2011 13:12
por deboralino » Sex Nov 25, 2011 13:12
LuizAquino escreveu:cicero escreveu:5) A solução será da forma:
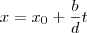
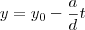
Onde t é um número inteiro.
Notem que a solução também pode estar na forma:

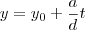
Onde t é um número inteiro.
Caro colega por gentileza você poderia me ajudar com equações diofantinas, eu verifique as sua dica mas ainda não consegui entender a resolução.
Meu email
lino-debora@bol.com.brAguardo e desde já agradeço sua atenção!
-
deboralino
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Qua Out 19, 2011 22:42
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por LuizAquino » Sex Nov 25, 2011 13:27
por LuizAquino » Sex Nov 25, 2011 13:27
deboralino escreveu:LuizAquino escreveu:cicero escreveu:5) A solução será da forma:
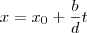
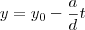
Onde t é um número inteiro.
Notem que a solução também pode estar na forma:

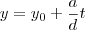
Onde t é um número inteiro.
Caro colega por gentileza você poderia me ajudar com equações diofantinas, eu verifique as sua dica mas ainda não consegui entender a resolução.
Meu email
lino-debora@bol.com.brAguardo e desde já agradeço sua atenção!
Há espalhado pela internet um vasto material sobre equações diofantinas! Para começar, eu recomendo que você dê uma olhada nas páginas abaixo:
Uma introdução às equações diofantinas do primeiro grau a duas variáveishttp://www.paulomarques.com.br/arq10-205.htmTeoria de números/Equações diofantinas - Wikilivroshttp://pt.wikibooks.org/wiki/Teoria_de_ ... iofantinasEu espero que esses materiais possam lhe ajudar.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Jomatema » Sáb Nov 26, 2011 17:20
por Jomatema » Sáb Nov 26, 2011 17:20
Como cursista e principalmente como professora, concordo que não devemos apenas copiar respostas dadas por outras pessoas, justamente por não aprendermos e ainda estas podem conter erros. Por outro lado, quando venho buscar auxílio num fórum como este, estou exercitando o meu direito de buscar meu aprendizado, pois em algumas semanas os exercícios resolvidos e os tópicos dos temas disponibilizados mais as orientações dos tutores são suficientes para elaborar minhas respostas. Entretanto, em outras semanas minhas dúvidas são tão grandes que nem essas três opções do curso são suficientes.
Gostei quando o tutor Cícero postou aqui uma orientação geral, depois de muito discutir com Ivan e entender nosso propósito nos fóruns, para o problema das equações diofantinas, foi justamente esse o caminho que segui baseada nas respostas que colegas postaram e buscando justificativas nos materiais do curso. Portanto, gostaria que os tutores não se apavorem com a disseminação de fóruns extra-curso, pois nós podemos muito bem sentarmos com um colega experiente e copiarmos uma resposta que ele dê, e só porque não está explícito não seremos condenados.
Tenho certeza que se tivermos mais abertura para explicitarmos nossas dúvidas dentro do AVA não precisaremos recorrer a outros recursos e Cícero, com todo respeito à sua pessoa e seu profissionalismo, não doeu nada escrever uma orientação aqui também!

Jomatema
-
Jomatema
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sex Nov 11, 2011 02:19
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
 por lidia1eliane » Dom Nov 27, 2011 23:06
por lidia1eliane » Dom Nov 27, 2011 23:06
cicero escreveu:Acredito que está na hora de vocês, cursistas do REDEFOR, terem um pouco mais de ética e não ficar pedindo respostas prontas das atividades propostas.
Sou orientador educacional do REDEFOR, e caso algum aluno da minha turma copie as repostas das atividades postadas neste site, ou em outro, não pensarei duas vezes para dar nota zero a elas.
Peço que cobrem mais dos seus respectivos orientadores, pois estes estão mais hábitos a darem ajudas sobre as atividades.
Tomem cuidado ao simplesmente copiarem, ou, como muitos fazem, mascarar as resposta fazenbdo mudanças gramaticais, isso não muda em nada.
Olá Cicero!
Eis o porquê procuramos informações na net antes de "torrarmos a paciência"
dos nossos tutores com nossas perguntas:

Considero isso sinais da "Quarta revolução na Educação". E mesmo tendo lido as dicas
dos colegas desse forum ainda tive que ler o material de apoio e a explicação que
você postou..ou seja, vocês tutores não precisam ter ciumes das novas tecnologias
porque há dúvidas e problemas para todos auxiliarem, mesmo o forum sendo uma grande
ajuda pode ficar sossegado, não deixaremos vocês em paz..rsr

Abraços

-
lidia1eliane
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Dom Nov 27, 2011 18:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por vitorullmann » Qui Fev 14, 2013 18:18
por vitorullmann » Qui Fev 14, 2013 18:18
cicero escreveu:Fique a vontade para tirar a dúvida do seu colega, e caso tenha dada alguma informação errada a respeito do assunto, eu poderei auxiliá-lo.
A pergunta do referido colega é querente,uma vez que o mesmo não postou simplesmente o enunciado dos execícios em si, mas somente pediu um auxílio em um conteúdo que poucos estão familiaraizados.
Deixo aqui uma dica para você e os demais a respeito desse assunto.
Dica:
As equações diofantinas do tipo

só tem sopluções inteiras em Z se, e seomente se, o

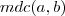
divide

, ou seja, se

for um múltiplo do
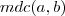
.
Do posto acima, podemos encontrar uma solução inteira para a equação diofantina

seguindo os seguintes passos:
1) Encontre o
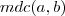
;
2) Verifique se
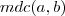
divide

;
3) Agora escreva a equação equivalente a

, onde
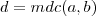
.
4) Encontre uma solução

e

, que será a menor possível. Isso pode ser feito por inspeção direta, ou atravéz do algoritmo da divisão euclidiana;
5) A solução será da forma:
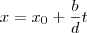
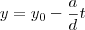
Onde

é um número inteiro.
Observe que as soluções acima resovem a equação diofantina

, faça o teste substituindo os valores acima nesta equação.
Exemplo:
1) A equação diofantina
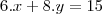
, tem solução:
Resposta: não, pois
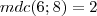
não divide
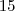
.
2) E a equção
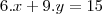
:
Reposta: sim, pois

divide
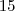
. Logo e equação dada pode ser escrita como:
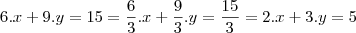
.
Então as soluções são:


Para t inteiro.
Tem como explicar um jeito de como resolver a parte 4, porque ela é a única que não consigo resolver, não sei como encontrar as respostas de x e y de nenhum desses métodos.
Apenas isso, nem por combinação linear, nem por Euclides. Enfim, não sei como. Obrigado!
-
vitorullmann
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Fev 13, 2013 18:48
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação Diofantina Quadrática
por CJunior » Qui Jun 26, 2014 10:53
- 1 Respostas
- 1638 Exibições
- Última mensagem por Russman

Qui Jun 26, 2014 21:31
Álgebra Elementar
-
- Como resolver equação diofantina utilizndo matrizes?
por joaofonseca » Qui Dez 13, 2012 17:25
- 2 Respostas
- 2952 Exibições
- Última mensagem por joaofonseca

Sex Dez 14, 2012 11:51
Teoria dos Números
-
- Equação - Dúvida básica sobre a proporcionalidade de equação
por FelipeGM » Qui Jan 12, 2012 19:05
- 4 Respostas
- 7712 Exibições
- Última mensagem por FelipeGM

Sáb Jan 14, 2012 13:16
Álgebra Elementar
-
- Equação - como montar a equação desse problema?
por _Manu » Qua Jul 04, 2012 03:37
- 7 Respostas
- 13203 Exibições
- Última mensagem por _Manu

Qui Jul 05, 2012 01:49
Sistemas de Equações
-
- [Equação polinomial] Ajuda com essa equação?
por Mkdj21 » Sáb Jan 26, 2013 16:19
- 1 Respostas
- 13011 Exibições
- Última mensagem por young_jedi

Dom Jan 27, 2013 17:15
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
onde C será 100 metros. Dessa forma irá encontrar o valor do raio.
e o comprimento da circunferência da 8ª raia utilizando a mesma fórmula anterior. (Porque calcular o comprimento da circunferência ? Justamente porque a pista possui duas semicircunferências iguais que juntando forma uma circunferência. Após calcular o comprimento da circunferência subtraia um valor do outro e obterá o resultado de que precisa.




 para comprimento da semicircunferência que é 100
para comprimento da semicircunferência que é 100 e ai sim você utiliza para o comprimento da circunferência 200
e ai sim você utiliza para o comprimento da circunferência 200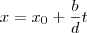
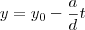

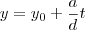



 só tem sopluções inteiras em Z se, e seomente se, o
só tem sopluções inteiras em Z se, e seomente se, o 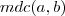 divide
divide  , ou seja, se
, ou seja, se  , onde
, onde 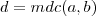 .
. e
e  , que será a menor possível. Isso pode ser feito por inspeção direta, ou atravéz do algoritmo da divisão euclidiana;
, que será a menor possível. Isso pode ser feito por inspeção direta, ou atravéz do algoritmo da divisão euclidiana; é um número inteiro.
é um número inteiro.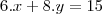 , tem solução:
, tem solução: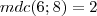 não divide
não divide 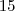 .
.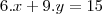 :
: divide
divide 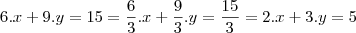 .
.
