 por beel » Dom Nov 20, 2011 22:33
por beel » Dom Nov 20, 2011 22:33
tomei como o "u" a raiz de t,da seguinte integrada
![\int_{1}^{ln5}(e\sqrt[]{t}/\sqrt[]{t})dt \int_{1}^{ln5}(e\sqrt[]{t}/\sqrt[]{t})dt](/latexrender/pictures/c84d2acc7402c7db0141ce7ade318f5c.png)
mas to em duvida se preciso substituir nos extremos dela tambem..meu resultado deu
1/2(5/2 - e/2)
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por LuizAquino » Seg Nov 21, 2011 10:10
por LuizAquino » Seg Nov 21, 2011 10:10
beel escreveu:tomei como o "u" a raiz de t,da seguinte integrada

mas to em duvida se preciso substituir nos extremos dela tambem..meu resultado deu
1/2(5/2 - e/2)
Fazendo a substituição

, temos que:
(i)

;
(ii) se t = 1, então u = 1 ;
(ii) se
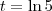
, então
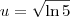
.
Sendo assim, obtemos que:
![\int_{1}^{\ln 5}\frac{e^\sqrt{t}}{\sqrt{t}}\,dt = \int_{1}^{\sqrt{\ln 5}}2e^u\,du = \left[2e^u\right]_1^{\sqrt{\ln 5}} = 2\left(e^{\sqrt{\ln 5}} - e\right) \int_{1}^{\ln 5}\frac{e^\sqrt{t}}{\sqrt{t}}\,dt = \int_{1}^{\sqrt{\ln 5}}2e^u\,du = \left[2e^u\right]_1^{\sqrt{\ln 5}} = 2\left(e^{\sqrt{\ln 5}} - e\right)](/latexrender/pictures/e1907097a3dc8480edb7be8689fa140d.png)
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integração por substituição
por manuoliveira » Seg Out 22, 2012 22:33
- 2 Respostas
- 1864 Exibições
- Última mensagem por manuoliveira

Ter Out 23, 2012 00:49
Cálculo: Limites, Derivadas e Integrais
-
- integração por substituição
por medeiro_aa » Seg Dez 07, 2015 18:35
- 2 Respostas
- 3399 Exibições
- Última mensagem por medeiro_aa

Qua Mar 02, 2016 11:44
Cálculo: Limites, Derivadas e Integrais
-
- MÉTODO DE INTEGRAÇÃO POR SUBSTITUIÇÃO
por HenriquePegorari » Dom Jul 25, 2010 17:26
- 3 Respostas
- 4622 Exibições
- Última mensagem por MarceloFantini

Ter Jul 27, 2010 12:54
Cálculo: Limites, Derivadas e Integrais
-
- [Integração por substituição] Ajuda, por favor?
por Ronaldobb » Dom Dez 16, 2012 18:44
- 2 Respostas
- 2139 Exibições
- Última mensagem por Ronaldobb

Dom Dez 16, 2012 18:47
Cálculo: Limites, Derivadas e Integrais
-
- [Integração por substituição] Ajuda, por favor?
por Ronaldobb » Dom Dez 16, 2012 21:26
- 1 Respostas
- 1620 Exibições
- Última mensagem por young_jedi

Dom Dez 16, 2012 21:52
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\int_{1}^{ln5}(e\sqrt[]{t}/\sqrt[]{t})dt \int_{1}^{ln5}(e\sqrt[]{t}/\sqrt[]{t})dt](/latexrender/pictures/c84d2acc7402c7db0141ce7ade318f5c.png)

![\int_{1}^{ln5}(e\sqrt[]{t}/\sqrt[]{t})dt \int_{1}^{ln5}(e\sqrt[]{t}/\sqrt[]{t})dt](/latexrender/pictures/c84d2acc7402c7db0141ce7ade318f5c.png)

 , temos que:
, temos que: ;
;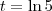 , então
, então 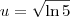 .
.![\int_{1}^{\ln 5}\frac{e^\sqrt{t}}{\sqrt{t}}\,dt = \int_{1}^{\sqrt{\ln 5}}2e^u\,du = \left[2e^u\right]_1^{\sqrt{\ln 5}} = 2\left(e^{\sqrt{\ln 5}} - e\right) \int_{1}^{\ln 5}\frac{e^\sqrt{t}}{\sqrt{t}}\,dt = \int_{1}^{\sqrt{\ln 5}}2e^u\,du = \left[2e^u\right]_1^{\sqrt{\ln 5}} = 2\left(e^{\sqrt{\ln 5}} - e\right)](/latexrender/pictures/e1907097a3dc8480edb7be8689fa140d.png)
