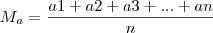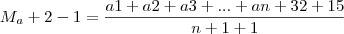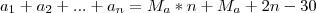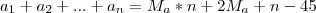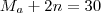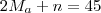por Cristina Lins » Sex Nov 18, 2011 10:56
por Cristina Lins » Sex Nov 18, 2011 10:56
Bom dia
Será que alguém pode me ajudar neste exercício?
Em uma turma de estudantes de Inglês, a média das idades dos alunos matriculados subiu 2 anos quando um aluno, que tinha 32 anos, foi matriculado. E caiu 1 ano quando outro aluno, que tinha 15 anos, matriculou-se. Quantos alunos tem essa turma, incluindo os dois últimos matriculados?
Um abraço
Cristina Lins
-
Cristina Lins
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Sex Nov 18, 2011 10:30
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por DanielFerreira » Seg Nov 28, 2011 20:21
por DanielFerreira » Seg Nov 28, 2011 20:21
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Média Aritmética
por gustavowelp » Seg Jun 28, 2010 11:17
- 1 Respostas
- 2371 Exibições
- Última mensagem por Douglasm

Seg Jun 28, 2010 12:09
Estatística
-
- Média aritmética
por Iolda Silveira » Qua Dez 10, 2014 23:01
- 1 Respostas
- 3085 Exibições
- Última mensagem por DanielFerreira

Qui Jan 01, 2015 21:53
Estatística
-
- média aritmética
por erick_martiliano » Qui Fev 26, 2015 13:53
- 1 Respostas
- 3413 Exibições
- Última mensagem por erick_martiliano

Qui Fev 26, 2015 14:04
Álgebra Elementar
-
- media aritmética ponderada
por rcpn » Ter Dez 02, 2014 21:11
- 1 Respostas
- 5298 Exibições
- Última mensagem por lucas_carvalho

Qua Dez 03, 2014 23:21
Álgebra Elementar
-
- Média aritmética e desvio padrão
por nayra » Qua Jun 16, 2010 23:21
- 1 Respostas
- 3440 Exibições
- Última mensagem por Neperiano

Dom Ago 14, 2011 14:24
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.