 por Aliocha Karamazov » Qui Nov 17, 2011 17:43
por Aliocha Karamazov » Qui Nov 17, 2011 17:43
Pessoal, ao resolver um exercício de física, no qual preciso encontrar

e

, apareceu um sistema que eu não sei resolver. Na situação física, ambos os ângulos são menores que

.
O sistema é:


Eu pensei em usar coisas como

, mas tenho a impressão de que essa não é a melhor maneira. Alguém pode me ajudar?
-
Aliocha Karamazov
- Usuário Parceiro

-
- Mensagens: 90
- Registrado em: Qua Mar 16, 2011 17:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física
- Andamento: cursando
 por TheoFerraz » Qui Nov 17, 2011 17:50
por TheoFerraz » Qui Nov 17, 2011 17:50
da primeira equação do seu sistema voce obtém que :
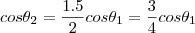
e como voce mesmo percebeu, temos que:
![cos {\theta}_{2}= \sqrt[]{1-sen{\theta}_{2}} = \frac{3}{4} cos{\theta}_{1} cos {\theta}_{2}= \sqrt[]{1-sen{\theta}_{2}} = \frac{3}{4} cos{\theta}_{1}](/latexrender/pictures/9c1698ee384ca2000414f4dbb4646fd5.png)
com isso, voce chega que:

se voce substituir ASSIM na segunda equação, nao vai dar em nada! esse cos de theta1 não nos ajuda... entaaaaao:
![sen{\theta}_{2} = 1-{\left( \frac{3}{4} \left(\sqrt[]{1 - sen{\theta}_{1}} \right) \right)}^{2} sen{\theta}_{2} = 1-{\left( \frac{3}{4} \left(\sqrt[]{1 - sen{\theta}_{1}} \right) \right)}^{2}](/latexrender/pictures/f50d66e30735220b107f848a288848ac.png)
dai

substituindo isso na segunda equação voce começa a obter resultados... continue dai
-
TheoFerraz
- Colaborador Voluntário

-
- Mensagens: 107
- Registrado em: Qua Abr 13, 2011 19:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Física
- Andamento: cursando
 por Aliocha Karamazov » Qui Nov 17, 2011 18:02
por Aliocha Karamazov » Qui Nov 17, 2011 18:02
TheoFerraz escreveu:
O seno não deveria estar ao quadrado aí?
-
Aliocha Karamazov
- Usuário Parceiro

-
- Mensagens: 90
- Registrado em: Qua Mar 16, 2011 17:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física
- Andamento: cursando
 por TheoFerraz » Qui Nov 17, 2011 18:09
por TheoFerraz » Qui Nov 17, 2011 18:09
SIM SIM SIM SIM SIM
em todos os momentos que eu coloquei:
![\sqrt[]{\left(1- sen{\theta}_{k} \right)} \sqrt[]{\left(1- sen{\theta}_{k} \right)}](/latexrender/pictures/c42fed679babd8596ebdd483105d6ce4.png)
era pra ter sido:
![\sqrt[]{\left(1- {sen}^{2}{\theta}_{k} \right)} \sqrt[]{\left(1- {sen}^{2}{\theta}_{k} \right)}](/latexrender/pictures/7d4f6065f1d549dffa40dbf8c796f3f0.png)
desculpe o erro, e obrigado a correção
.
-
TheoFerraz
- Colaborador Voluntário

-
- Mensagens: 107
- Registrado em: Qua Abr 13, 2011 19:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Física
- Andamento: cursando
 por Aliocha Karamazov » Qui Nov 17, 2011 18:13
por Aliocha Karamazov » Qui Nov 17, 2011 18:13
Eu que agradeço pelo ajuda. Vou continuar aqui.
-
Aliocha Karamazov
- Usuário Parceiro

-
- Mensagens: 90
- Registrado em: Qua Mar 16, 2011 17:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física
- Andamento: cursando
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- sistemas de equãções
por Rejane Sampaio » Sex Set 12, 2008 23:54
- 1 Respostas
- 2663 Exibições
- Última mensagem por admin

Ter Set 16, 2008 20:31
Estatística
-
- Sistemas de equações
por Danilo Dias Vilela » Qua Set 09, 2009 17:34
- 1 Respostas
- 1274 Exibições
- Última mensagem por Molina

Qua Set 09, 2009 17:54
Sistemas de Equações
-
- Sistemas de equações
por Danilo Dias Vilela » Qua Set 09, 2009 21:19
- 1 Respostas
- 1437 Exibições
- Última mensagem por Elcioschin

Qua Set 09, 2009 22:27
Sistemas de Equações
-
- Sistemas de equações
por Danilo Dias Vilela » Qua Set 09, 2009 23:55
- 1 Respostas
- 2300 Exibições
- Última mensagem por Molina

Qui Set 10, 2009 14:15
Sistemas de Equações
-
- Sistemas de equações
por Danilo Dias Vilela » Qui Set 10, 2009 00:25
- 2 Respostas
- 2267 Exibições
- Última mensagem por RICI

Sex Ago 24, 2012 11:58
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 e
e  , apareceu um sistema que eu não sei resolver. Na situação física, ambos os ângulos são menores que
, apareceu um sistema que eu não sei resolver. Na situação física, ambos os ângulos são menores que  .
.

 , mas tenho a impressão de que essa não é a melhor maneira. Alguém pode me ajudar?
, mas tenho a impressão de que essa não é a melhor maneira. Alguém pode me ajudar?
 e
e  , apareceu um sistema que eu não sei resolver. Na situação física, ambos os ângulos são menores que
, apareceu um sistema que eu não sei resolver. Na situação física, ambos os ângulos são menores que  .
.

 , mas tenho a impressão de que essa não é a melhor maneira. Alguém pode me ajudar?
, mas tenho a impressão de que essa não é a melhor maneira. Alguém pode me ajudar?
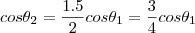
![cos {\theta}_{2}= \sqrt[]{1-sen{\theta}_{2}} = \frac{3}{4} cos{\theta}_{1} cos {\theta}_{2}= \sqrt[]{1-sen{\theta}_{2}} = \frac{3}{4} cos{\theta}_{1}](/latexrender/pictures/9c1698ee384ca2000414f4dbb4646fd5.png)

![sen{\theta}_{2} = 1-{\left( \frac{3}{4} \left(\sqrt[]{1 - sen{\theta}_{1}} \right) \right)}^{2} sen{\theta}_{2} = 1-{\left( \frac{3}{4} \left(\sqrt[]{1 - sen{\theta}_{1}} \right) \right)}^{2}](/latexrender/pictures/f50d66e30735220b107f848a288848ac.png)



![\sqrt[]{\left(1- sen{\theta}_{k} \right)} \sqrt[]{\left(1- sen{\theta}_{k} \right)}](/latexrender/pictures/c42fed679babd8596ebdd483105d6ce4.png)
![\sqrt[]{\left(1- {sen}^{2}{\theta}_{k} \right)} \sqrt[]{\left(1- {sen}^{2}{\theta}_{k} \right)}](/latexrender/pictures/7d4f6065f1d549dffa40dbf8c796f3f0.png)




 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.