Olá para todos.
Quer dizer que quando eu encontro "u", segundo alguns amigos estão explicando constantemente, eu posso substituir.
Por exemplo: Se eu tiver uma tabela que tenha dy/du igual a alguma coisa, eu posso substituir o "u" por qualquer função e derivar em relação a u, só para exemplificar.
Mais um exemplo: Integral de 1/(logx)²dx, eu posso substituir por integral de 1/u²du?.
O mesmo para integralx(x)²dx = integralxx²dx = integralx(x²)dx ou tem alguma diferença? por exemplo: integralx(x²)dx = integralx(u²)du? = integralx(u)² ou algo semelhante?





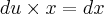
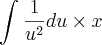




 .
.



