Estou encontrando algumas dúvidas na resolução do problema abaixo. Se alguém puder me ajudar, agradeço .
--> Existe um número real x tal que o quociente
é um número imaginário puro. Determine o simétrico de x.Bom, eu resolvi a divisão dos números complexos:
e encontrei as seguintes respostas: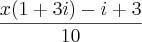 
(Tirando o Fator Comum de 
) 
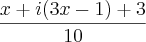(Tirando o Fator Comum de 
)Analisando "Tirando o Fator Comum de
" para que seja imaginário puro, a parte real 
deverá ser 
(Portanto 
)Até aqui está certo???
Como prosseguir???
Até mais
, pois eu dividir um número pelo outro é mesma coisa que multiplicar esse número pelo conjugado desse outro.
)..
.
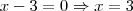
![i^2 = (\sqrt[2]{-1})^2 = -1](/latexrender/pictures/51889bb41206c7cf9efc7ee4909bbf2c.png "i^2 = (\sqrt[2]{-1})^2 = -1")
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")