Um artista plástico deseja fazer um painel. Para tanto, deve preencher completamente a superfície de um quadro, no formato de um triangulo equilatero cujo lado mede 48cm, com pequenos triangulos equiláteros multicoloridos, cujos lados medem 1cm. Se esses pequenos triangulos forem pintados em tons diferentes, quantas tonalidades serão necessárias?
Eu tentei achando a área do triangulo, calculando a altura de um triangulo equilatero mas nao quer dar certo.


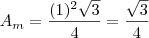
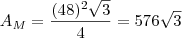
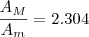


 .
.
 :
: