 por Andreza » Dom Out 23, 2011 11:42
por Andreza » Dom Out 23, 2011 11:42
Um artista plástico deseja fazer um painel. Para tanto, deve preencher completamente a superfície de um quadro, no formato de um triangulo equilatero cujo lado mede 48cm, com pequenos triangulos equiláteros multicoloridos, cujos lados medem 1cm. Se esses pequenos triangulos forem pintados em tons diferentes, quantas tonalidades serão necessárias?
Eu tentei achando a área do triangulo, calculando a altura de um triangulo equilatero mas nao quer dar certo.
-
Andreza
- Colaborador Voluntário

-
- Mensagens: 100
- Registrado em: Sáb Out 22, 2011 11:10
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Licenc. Plena Matemática
- Andamento: formado
 por LuizAquino » Sáb Nov 12, 2011 09:11
por LuizAquino » Sáb Nov 12, 2011 09:11
Andreza escreveu:Um artista plástico deseja fazer um painel. Para tanto, deve preencher completamente a superfície de um quadro, no formato de um triangulo equilatero cujo lado mede 48cm, com pequenos triangulos equiláteros multicoloridos, cujos lados medem 1cm. Se esses pequenos triangulos forem pintados em tons diferentes, quantas tonalidades serão necessárias?
Eu tentei achando a área do triangulo, calculando a altura de um triangulo equilatero mas nao quer dar certo.
Área do triângulo equilátero menor:
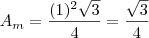
Área do triângulo equilátero maior:
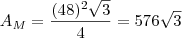
Quantos triângulos menores pode haver dentro do triângulo maior:
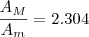
Portanto, a quantidade de tonalidades deve ser 2.304.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Andreza » Sáb Nov 12, 2011 09:56
por Andreza » Sáb Nov 12, 2011 09:56
Muito obrigada mesmo eu aqui quebrando a cabeça para resolver este exercício e nunca imaginei q era só calcula a área e depois dividir. Deus abençoe muito vc pela enorme ajuda.
-
Andreza
- Colaborador Voluntário

-
- Mensagens: 100
- Registrado em: Sáb Out 22, 2011 11:10
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Licenc. Plena Matemática
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Triângulo Equilatéro
por Cleyson007 » Seg Mai 25, 2009 08:15
- 6 Respostas
- 3127 Exibições
- Última mensagem por ginrj

Dom Jun 07, 2009 20:39
Geometria Plana
-
- Triangulo Equilatero e GA
por isabelamiaki » Seg Abr 05, 2010 13:19
- 1 Respostas
- 2765 Exibições
- Última mensagem por Elcioschin

Seg Abr 05, 2010 22:09
Geometria Analítica
-
- Triângulo Equilátero
 por Pri Ferreira » Qua Mar 21, 2012 14:30
por Pri Ferreira » Qua Mar 21, 2012 14:30
- 1 Respostas
- 1801 Exibições
- Última mensagem por LuizAquino

Sáb Mar 31, 2012 13:56
Geometria Plana
-
- triângulo equilátero
por zenildo » Qua Jul 15, 2015 11:13
- 4 Respostas
- 7373 Exibições
- Última mensagem por nakagumahissao

Qui Jul 16, 2015 03:34
Geometria Plana
-
- Triângulo equilátero ( urgente)
 por Carlos28 » Seg Mar 17, 2014 12:36
por Carlos28 » Seg Mar 17, 2014 12:36
- 2 Respostas
- 1746 Exibições
- Última mensagem por Carlos28

Ter Mar 18, 2014 15:24
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


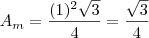
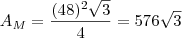
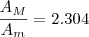



 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.