





 . As regras de inferência são os métodos a serem utilizados no processo de validação deste argumento. Isso é lógica proposicional, um assunto que está sendo abordado no meu curso de Licenciatura em Informática. Espero que vc possa me ajudar. Obrigado pela atenção. Também agradeço ao Neperiano pela dica de memorização. Eu já tentei auxílio com internet, livros, mas ainda assim continua complicado.
. As regras de inferência são os métodos a serem utilizados no processo de validação deste argumento. Isso é lógica proposicional, um assunto que está sendo abordado no meu curso de Licenciatura em Informática. Espero que vc possa me ajudar. Obrigado pela atenção. Também agradeço ao Neperiano pela dica de memorização. Eu já tentei auxílio com internet, livros, mas ainda assim continua complicado.



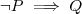 e
e  . Daí, podemos concluir
. Daí, podemos concluir 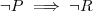 . Pela negação, podemos afirmar que
. Pela negação, podemos afirmar que  .
.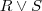 . Para que esta afirmação seja verdadeira, temos três casos: R pode ser verdadeiro e S não; R pode ser verdadeiro e S também; R não é verdadeiro mas S é. Em outras palavras pelo menos um deles tem que ser verdadeiro. Por isso dizemos que em matemática o "ou" é inclusivo, ao invés da fala comum que usamos como exclusivo (exemplo: "você quer café normal ou descafeinado?").
. Para que esta afirmação seja verdadeira, temos três casos: R pode ser verdadeiro e S não; R pode ser verdadeiro e S também; R não é verdadeiro mas S é. Em outras palavras pelo menos um deles tem que ser verdadeiro. Por isso dizemos que em matemática o "ou" é inclusivo, ao invés da fala comum que usamos como exclusivo (exemplo: "você quer café normal ou descafeinado?"). . Ou seja, R de fato acontece e portanto obrigatoriamente a relação
. Ou seja, R de fato acontece e portanto obrigatoriamente a relação 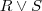 é satisfeita, não interessando se S acontece ou não, portanto podemos afirmar que
é satisfeita, não interessando se S acontece ou não, portanto podemos afirmar que  . Analogamente,
. Analogamente,  , porém neste caso o que somos levados a ver que S acontece mas R não, pela condição anterior.
, porém neste caso o que somos levados a ver que S acontece mas R não, pela condição anterior.



Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.