 por Neperiano » Ter Mai 12, 2009 21:04
por Neperiano » Ter Mai 12, 2009 21:04
Ola
A questão é bem simples, monto ela fácil mas não consigo chegar ao resultado, que concerteza é esse.
Ai vai:
O raio da base, a altura e a geratriz de um cone reto constituiem, nessa ordem uma PA de razão 1. Calcule a área total do cone.( Resposta = 75,36 aproximadamente )
r = x-1
h = x
g = x + 1
Dai uso a formula
{}g^2{}={}r^2 + h^2{}
Mas naum dah certo, não chega a esse resultado
Desde ja agradeço
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por admin » Ter Mai 12, 2009 21:31
por admin » Ter Mai 12, 2009 21:31
Olá
Maligno.
Realmente, a resposta é aproximadamente o que você citou.
Mais precisamente:
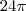
.
Atenção para os seguintes itens e chegará ao resultado:
-a "fórmula" que você citou é o teorema de Pitágoras para o triângulo retângulo relacionado no cone reto.
Por substituição, deixe apenas

na expressão e encontre

.
-Também por substituição nas expressões dadas da P.A., encontre

e

.
-Calcule a
área lateral 
do cone (escrevi um tópico no fórum comentando como obtemos esta expressão):

-Some a
área da base 
à
área lateral 
para obter a
área total 
:
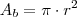
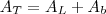
Até!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por Molina » Ter Mai 12, 2009 21:44
por Molina » Ter Mai 12, 2009 21:44
É.. Eu ia falar isso mesmo que o fábio informou, que este valor que você acharia com um

, por isso o valor aproximado.
Lembrando que
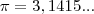
Abraços!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por admin » Ter Mai 12, 2009 21:54
por admin » Ter Mai 12, 2009 21:54
Olá Molina!
Embora eu tenho as minhas suspeitas de que foi apenas esquecimento de somar a área da base.
Abraços!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por Neperiano » Qua Mai 13, 2009 15:00
por Neperiano » Qua Mai 13, 2009 15:00
Ola
O problema eh q eu naum enontro h=4, os numeros cortam tudo olha soh
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por Neperiano » Qui Mai 14, 2009 17:13
por Neperiano » Qui Mai 14, 2009 17:13
Ola
A professora mostro essa questão hoje demanha, mas obrigado mesmo assim
Ate
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
Voltar para Geometria Espacial
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Cone (ITA - SP)
 por Ananda » Ter Fev 26, 2008 20:07
por Ananda » Ter Fev 26, 2008 20:07
- 3 Respostas
- 9655 Exibições
- Última mensagem por admin

Qua Fev 27, 2008 13:08
Geometria Espacial
-
- Cone
por GABRIELA » Sex Fev 12, 2010 16:09
- 2 Respostas
- 1852 Exibições
- Última mensagem por GABRIELA

Qui Fev 18, 2010 14:59
Geometria Espacial
-
- Cone
por DanielFerreira » Qua Jun 23, 2010 16:25
- 1 Respostas
- 1535 Exibições
- Última mensagem por MarceloFantini

Qui Jun 24, 2010 00:01
Geometria Espacial
-
- cone
 por creberson » Ter Ago 21, 2012 10:18
por creberson » Ter Ago 21, 2012 10:18
- 4 Respostas
- 2673 Exibições
- Última mensagem por Cleyson007

Qua Ago 22, 2012 10:03
Geometria Espacial
-
- cone
por creberson » Ter Ago 21, 2012 22:11
- 0 Respostas
- 1072 Exibições
- Última mensagem por creberson

Ter Ago 21, 2012 22:11
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


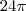 .
. na expressão e encontre
na expressão e encontre  .
. e
e  .
. do cone (escrevi um tópico no fórum comentando como obtemos esta expressão):
do cone (escrevi um tópico no fórum comentando como obtemos esta expressão):
 à
à  :
: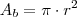
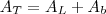

 , por isso o valor aproximado.
, por isso o valor aproximado.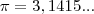


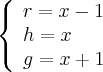
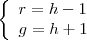
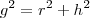
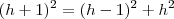

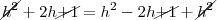

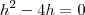

 ou
ou  pois existe o cone)
pois existe o cone)




