 por beel » Dom Nov 06, 2011 17:40
por beel » Dom Nov 06, 2011 17:40
em relaçao a essa funçao

preciso encontrar os intervalos onde ela é concava para cima, ai eu derivei a primeira vez e derivei a segunda mas nao to conseguindo simplificar...ela ficou assim

. Os candidatos a pontos de inflexao, sao os pontos onde a derivada segunda nao existe ou da zero certo?fiz umas contas e meu ponto deu

mas estou muito em duvida
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por LuizAquino » Qua Nov 09, 2011 08:54
por LuizAquino » Qua Nov 09, 2011 08:54
beel escreveu:em relaçao a essa funçao

preciso encontrar os intervalos onde ela é concava para cima, ai eu derivei a primeira vez e derivei a segunda mas nao to conseguindo simplificar...ela ficou assim

.
Note que:

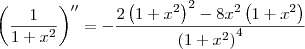 Dica:
Dica: no numerador da fração que representa a segunda derivada, comece a simplificação colocando o termo
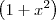
em evidência.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [derivada] derivada pela definição da secante
por TheKyabu » Sáb Out 27, 2012 23:24
- 2 Respostas
- 10878 Exibições
- Última mensagem por TheKyabu

Dom Out 28, 2012 11:44
Cálculo: Limites, Derivadas e Integrais
-
- Derivada pela Definiçao
por PeIdInHu » Sáb Mai 22, 2010 17:24
- 1 Respostas
- 2197 Exibições
- Última mensagem por admin

Sáb Mai 22, 2010 18:24
Cálculo: Limites, Derivadas e Integrais
-
- Derivada pela definiçao
por tumiattibrz » Sex Mai 27, 2011 17:17
- 3 Respostas
- 2508 Exibições
- Última mensagem por LuizAquino

Sáb Mai 28, 2011 12:28
Cálculo: Limites, Derivadas e Integrais
-
- derivada pela definiçao
por paula luna » Sex Jun 10, 2011 04:41
- 2 Respostas
- 2278 Exibições
- Última mensagem por Fabio Cabral

Sex Jun 10, 2011 11:23
Cálculo: Limites, Derivadas e Integrais
-
- Derivada pela definição
por core » Qua Out 16, 2013 02:15
- 1 Respostas
- 1750 Exibições
- Última mensagem por Taka

Sáb Nov 02, 2013 21:26
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

 . Os candidatos a pontos de inflexao, sao os pontos onde a derivada segunda nao existe ou da zero certo?fiz umas contas e meu ponto deu
. Os candidatos a pontos de inflexao, sao os pontos onde a derivada segunda nao existe ou da zero certo?fiz umas contas e meu ponto deu  mas estou muito em duvida
mas estou muito em duvida


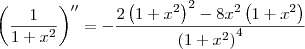
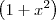 em evidência.
em evidência.
