Primeiramente, eu gostaria de agradecer muito o espaço! Minha dúvida é sobre como determinar Z em certos casos, como por exemplo, quando este é elevado ao quadrado(Z²)
Vou tentar ser mais claro, por exemplo:
Quando eu tenho Z3 = 2+3i e Z2 = 5+3i, e eu preciso determinar a conta Z3² + Z2, eu simplesmente não tenho certeza como efetuar o cálculo corretamente. Nesse exemplo eu resolvi essa questão da seguinte maneira:
Z3² + Z2 = (2,3).(2,3)+(5,3)i = (4-6,6+9)+(5,3)i = (-2,15)+(5,3)i = (-2+5)+(15+3)i = Z3²+Z2= 3+18i
O que fiz aí, foi simplesmente tentar seguir um exemplo q meu professor fez durante a aula, mas não consegui entender nada, acho que fiz alguma coisa errada ou tudo rs.
Também, não sei como fazer equações do tipo Z1+Z2-Z3... Mas nesse tipo de equação, acho que entendi, só não me sinto muito seguro ao calculá-lo. Vou tentar explicar como eu faria um exercício desse tipo
Por exemplo, se eu tenho Z1+Z2 = 7+1i, então acho q fica fácil é só trocar Z1+Z2 por 7+1i depois é separar o termo real do imaginário, ficando assim:
(7+1)-(2+3)i = 8-5i
Gostaria muito de tirar essas dúvidas, nessas duas contas, eu praticamente tive q improvisar uma maneira de resolvê-las, mas não tenho certeza se fiz da maneira certa, por preciso muito que alguém me ajude! Gostaria de mostrar também um video aula que acompanhei atentamente e que realmente consegui aprender muito, mas infelizmente, não ensina como resolver questões como essas que aprensentei. Mas uma vez, muito obrigado pela atenção, espero que alguem me ajude logo, grato!


 , então
, então 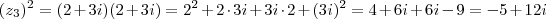 .
. 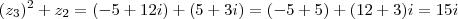 .
.


 .
.
 :
: