Estou encontrando dificuldade na resolução do problema abaixo
 Gostaria que alguém me auxiliasse. Desde já agradeço pela atenção
Gostaria que alguém me auxiliasse. Desde já agradeço pela atenção 
--> Em uma fazenda produtora de soja duas colheitadeiras A e B são utilizadas para a colheita da produção. Quando trabalham juntas conseguem fazer toda a colheita em 72 horas. Porém, utilizando apenas a colheitadeira A, em 120 horas. Se o produtor utilizar apenas a colheitadeira B, toda a colheita será feita em:
(A) 180 horas
(B) 165 horas
(C) 157 horas
(D) 192 horas



 do exercício.
do exercício.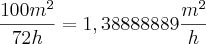 para saber quanto m² as duas juntas colhiam por hora.
para saber quanto m² as duas juntas colhiam por hora.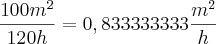
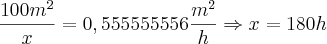 .
.

 o rendimento das máquinas.
o rendimento das máquinas.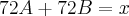
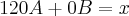
 não é igual ao rendimento da máquina
não é igual ao rendimento da máquina  , por esse motivo vou chamá-lo de
, por esse motivo vou chamá-lo de  .
.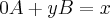
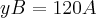
![72(A+B)=120A
[tex]A+B=1,66A 72(A+B)=120A
[tex]A+B=1,66A](/latexrender/pictures/99e770bca0e4cb0431c7b0129a5f3062.png)
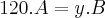
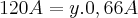
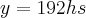
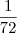 do trabalho por hora. A segunda sozinha faz
do trabalho por hora. A segunda sozinha faz 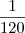 por hora. A primeira sozinha faz:
por hora. A primeira sozinha faz: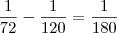
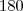 horas sozinha.
horas sozinha.



