 por Andreza » Ter Nov 01, 2011 12:31
por Andreza » Ter Nov 01, 2011 12:31
Boa tarde,
Estou estudando para prestar concurso, pois fiz matemática e pós, mas estou encontrando muitas dificuldades diante das questões propostas pela banca organizadora FCC, este exercício q estou postando na verdade nem sei como começar, pois nao foram dados nenhum valores pra x. Espero q vcs possam me ajudar e se algum de vcs moderadores, forem professores de aulas particulares favor entrar em contato q pelo jeito eu estou precisando de umas aulas extras. Aguardo resposta, desde já fico muito grata. Obs. : Eu já comprei curso on line e apostilas, mas mesmo assim está muito difícil para o nível do concurso.
Quais são as raízes da equação sen²x - ( 2sen x cos x - cos²x) = 0 em [0,2pi] ?
-
Andreza
- Colaborador Voluntário

-
- Mensagens: 100
- Registrado em: Sáb Out 22, 2011 11:10
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Licenc. Plena Matemática
- Andamento: formado
 por Neperiano » Ter Nov 01, 2011 14:19
por Neperiano » Ter Nov 01, 2011 14:19
Ola
O que o Marcelo fez está correto:
MarceloFantini escreveu:Andreza, desconsidere a resposta do Neperiano. Primeiro, é interessante lembrar algumas relações trigonométricas úteis:
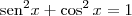
e
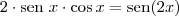
. Desta forma, a equação se torna:
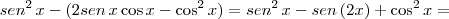
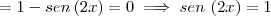
.
Isto significa que
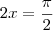
e daí
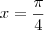
.
Atenciosamente
Editado pela última vez por
Neperiano em Ter Nov 01, 2011 15:18, em um total de 1 vez.
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por MarceloFantini » Ter Nov 01, 2011 15:11
por MarceloFantini » Ter Nov 01, 2011 15:11
Andreza, desconsidere a resposta do Neperiano. Primeiro, é interessante lembrar algumas relações trigonométricas úteis:
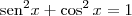
e
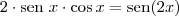
. Desta forma, a equação se torna:
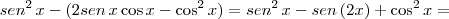
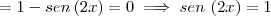
.
Isto significa que
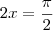
e daí
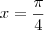
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Andreza » Ter Nov 01, 2011 18:04
por Andreza » Ter Nov 01, 2011 18:04
Muito obrigada Marcelo.
Na verdade eu só conhecia a primeira relação fundamental q vc mencionou na resolução do exercício.
Agora vou incluir a segunda nos outros exercícios q estou estudando.
Sendo x =45 graus como faço para encontar a segunda raiz?
-
Andreza
- Colaborador Voluntário

-
- Mensagens: 100
- Registrado em: Sáb Out 22, 2011 11:10
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Licenc. Plena Matemática
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [raízes de números complexos] Raízes de uma equação com grau
por karenfreitas » Seg Ago 22, 2016 19:08
- 1 Respostas
- 8112 Exibições
- Última mensagem por adauto martins

Sáb Ago 27, 2016 16:11
Números Complexos
-
- Raízes da equação
por Andreza » Seg Nov 14, 2011 14:47
- 1 Respostas
- 1164 Exibições
- Última mensagem por MarceloFantini

Seg Nov 14, 2011 19:19
Funções
-
- Equação Raízes
por LuizCarlos » Seg Mai 07, 2012 13:59
- 2 Respostas
- 1373 Exibições
- Última mensagem por Cleyson007

Seg Mai 07, 2012 14:50
Álgebra Elementar
-
- Raízes da equação
 por joohhn » Qua Mai 18, 2016 17:11
por joohhn » Qua Mai 18, 2016 17:11
- 1 Respostas
- 1509 Exibições
- Última mensagem por joohhn

Qua Mai 18, 2016 20:46
Trigonometria
-
- equação de raízes complexas
por MariPC » Sáb Ago 15, 2009 15:56
- 1 Respostas
- 2213 Exibições
- Última mensagem por Felipe Schucman

Sáb Ago 15, 2009 17:35
Números Complexos
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


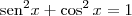 e
e 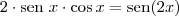 . Desta forma, a equação se torna:
. Desta forma, a equação se torna: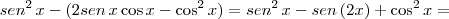
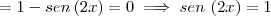 .
.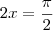 e daí
e daí 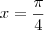 .
.

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.