
como resolver? tentei por L'Hospital e derivei uma vez mas não esta dando certo




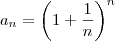 é limitada e estritamente crescente. Logo, ela converge. O número para o qual ela converge é o número de Euler e.
é limitada e estritamente crescente. Logo, ela converge. O número para o qual ela converge é o número de Euler e. também existe e é igual a e. Ou seja, o limite da função
também existe e é igual a e. Ou seja, o limite da função  é igual ao limite da sequência
é igual ao limite da sequência 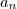 .
.
Aliocha Karamazov escreveu:Esse limite não é calculado como os outros.
beel escreveu:como resolver? tentei por L'Hospital e derivei uma vez mas não esta dando certo
 temos que
temos que 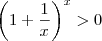 .
.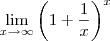 . Pelo que expliquei acima, devemos ter
. Pelo que expliquei acima, devemos ter  .
.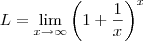
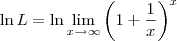

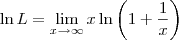
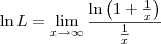
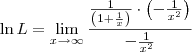
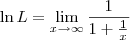




LuizAquino escreveu:Aliocha Karamazov escreveu:Esse limite não é calculado como os outros.
Uma vez provada a Regra de L'Hospital, podemos usá-la para calcular esse limite.

Aliocha Karamazov escreveu:Eu só achei que seria estranho utilizar o logaritmo na base e para calcular e sem nem ter definido esse número.

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.