
como resolver? tentei por L'Hospital e derivei uma vez mas não esta dando certo




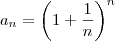 é limitada e estritamente crescente. Logo, ela converge. O número para o qual ela converge é o número de Euler e.
é limitada e estritamente crescente. Logo, ela converge. O número para o qual ela converge é o número de Euler e. também existe e é igual a e. Ou seja, o limite da função
também existe e é igual a e. Ou seja, o limite da função  é igual ao limite da sequência
é igual ao limite da sequência 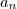 .
.
Aliocha Karamazov escreveu:Esse limite não é calculado como os outros.
beel escreveu:como resolver? tentei por L'Hospital e derivei uma vez mas não esta dando certo
 temos que
temos que 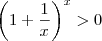 .
.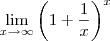 . Pelo que expliquei acima, devemos ter
. Pelo que expliquei acima, devemos ter  .
.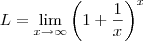
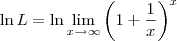

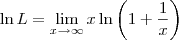
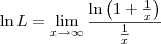
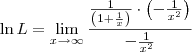
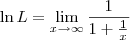




LuizAquino escreveu:Aliocha Karamazov escreveu:Esse limite não é calculado como os outros.
Uma vez provada a Regra de L'Hospital, podemos usá-la para calcular esse limite.

Aliocha Karamazov escreveu:Eu só achei que seria estranho utilizar o logaritmo na base e para calcular e sem nem ter definido esse número.

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)