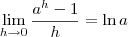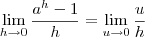Como a variável é
h,
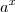
é uma constante e, portanto, você pode "tirar" de limite.
A sua dúvida, então, é calcular

Dessa forma, é difícil mesmo calcular. Precisamos utilizar algum artifício.
Vamos fazer

. Perceba que, quando
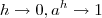
(quando
h tende a zero,
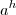
tende a 1, pois qualquer número real elevado a zero é igual a 1).
Dessa forma,

Podemos escrever:
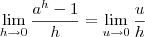
.
Agora, precisamos escrever
h em função da nova variável
u que nós colocamos. Note que:

.
Podemos aplicar a função logrtitmo natural em ambos os lados da equação:
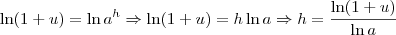
Note que utilizei uma propriedade logaritmica conhecida como "regra do tombo". Se tiver alguma dúvida, revise isso.
Segue-se que:

Perceba que
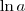
"saiu" do limite também. Precisamos mostrar, agora, que
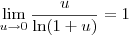
Vamos dividir tanto o numerador como o denominador por

, o que não muda o valor do nosso limite. Temos, então:

.
Novamente, utilizamos a "regra do tombo". Na verdadem, fizemos o inverso da "regra do tombo", pois colocamos o número que multiplica o expoente para o logaritmo.
Estamos no fim, só precisamos de mais um resultado. Vou "dar" o resultado, cuja demonstração é simples, para não deixar minha postagem ainda mais extensa. Assumindo que isso é verdade, terminamos nossa demonstração. Se você tiver compreendido tudo que eu fiz até agora, me avise que eu demonstro o que vou dizer a seguir (ou tente você mesmo). A informação é a seguinte:

Com isso, temos que:

, pois

Conluímos, então, que
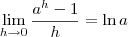
Talvez eu tenha "explicado demais". Nos livros de cálculo, isso é bem mais direto. Mas eu fiz assumindo que você não conhecia nenhum resultado utilizado. Avise se teve dúvida em algum ponto, que eu explico.
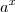 , utilizando a definição de derivada.
, utilizando a definição de derivada.![\frac{d}{d_{x}}\hspace{5}a^x=\lim_{h \mapsto 0}\left [\frac{a^{x+h}-a^x}{h} \right ] \frac{d}{d_{x}}\hspace{5}a^x=\lim_{h \mapsto 0}\left [\frac{a^{x+h}-a^x}{h} \right ]](/latexrender/pictures/fc54113208df1cc1afad6281e1bc48cb.png)
![\frac{d}{d_{x}}=a^x \cdot \lim_{h \mapsto 0} \left [ \frac{a^h-1}{h} \right ] \frac{d}{d_{x}}=a^x \cdot \lim_{h \mapsto 0} \left [ \frac{a^h-1}{h} \right ]](/latexrender/pictures/28205cf412cfd2a86977d2eaf35945dd.png)
 . Mas como eu posso demonstrar isso, utilizando principios básicos de Algebra e as propriedades dos exponenciais e logaritmos?
. Mas como eu posso demonstrar isso, utilizando principios básicos de Algebra e as propriedades dos exponenciais e logaritmos?


 . Perceba que, quando
. Perceba que, quando 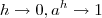 (quando
(quando 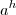 tende a 1, pois qualquer número real elevado a zero é igual a 1).
tende a 1, pois qualquer número real elevado a zero é igual a 1).
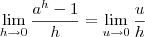 .
.  .
.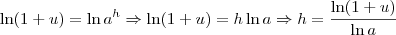

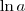 "saiu" do limite também. Precisamos mostrar, agora, que
"saiu" do limite também. Precisamos mostrar, agora, que 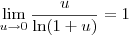
 , o que não muda o valor do nosso limite. Temos, então:
, o que não muda o valor do nosso limite. Temos, então: .
. 
 , pois
, pois