 por gomusalie » Qui Out 27, 2011 15:53
por gomusalie » Qui Out 27, 2011 15:53
O vertice da parabola y= ax2 + bx + c e o ponto (-2,3). Sabendo que 5 e a ordenada onde a curva corta o eixo vertical, podemos afirmar que
(A) a>1, b<1 e c<4
(B) a>2, b>3 e c>4
(C) a<1, b<1 e c>4
(D) a<1, b>1 e c>4
(E) a<1, b<1 e c<4
________________________________________________________________________________________________
Bom, para mim, só falta o valor do b. Olha como eu fiz:
Bom, Tracei o grafico, e marquei os pontos (-2,3) e deu no quarto quadrante. Bom, 5 é o valor de "c" pois é o valor em que corta o eixo de y, certo? com isso ele cortando o y num valor positivo de 5, então para ser uma função, a lógica é que a concavidade é voltada para baixo, então "a" é negativo, ou seja a<1. Agora o "c" --> Como o valor que corta o eixo y é 5, eu acho que o "c" é 5, portanto c>4. Agora eu fico na duvida de como achar o "b". Obg e aguardo resposta!
-
gomusalie
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qui Out 27, 2011 15:33
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por angieluis » Qui Out 27, 2011 19:14
por angieluis » Qui Out 27, 2011 19:14
Uma outra forma de apresentar uma parabola (função quadratica) é:

em que (h,k) são as coordenadas do vertice da parabola.
assim temos:

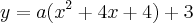

(1)
no ponto (0,5) temos, substituindo x e y:
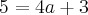
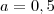
voltando a (1) e substituindo agora a temos:

onde está muito claro os valores de a, b e c.
Resposta: D
-
angieluis
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qui Out 27, 2011 18:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matematica
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- estudo de sinais de uma equação de 3º grau
por ygor_macabu » Ter Mai 01, 2012 02:00
- 1 Respostas
- 7095 Exibições
- Última mensagem por Guill

Ter Mai 01, 2012 09:12
Polinômios
-
- Estudo da função
por Harzeus » Seg Jan 10, 2011 13:58
- 1 Respostas
- 1183 Exibições
- Última mensagem por Neperiano

Qui Out 27, 2011 15:27
Funções
-
- Função ( Estudo do sinal )
por clara » Dom Jun 21, 2009 20:55
- 1 Respostas
- 5317 Exibições
- Última mensagem por Molina

Seg Jun 22, 2009 12:57
Funções
-
- Estudo de uma Função Logaritmica
por Ice » Dom Jul 24, 2011 18:06
- 3 Respostas
- 1748 Exibições
- Última mensagem por LuizAquino

Dom Jul 24, 2011 21:30
Logaritmos
-
- Estudo da [continuidade] de uma função
por Teh_eng » Qui Mai 03, 2012 13:43
- 1 Respostas
- 1369 Exibições
- Última mensagem por Russman

Qui Mai 03, 2012 14:52
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 em que (h,k) são as coordenadas do vertice da parabola.
em que (h,k) são as coordenadas do vertice da parabola.
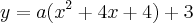
 (1)
(1)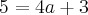
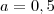
 onde está muito claro os valores de a, b e c.
onde está muito claro os valores de a, b e c.![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.