Gostaria de uma ajuda para resolver a seguinte integral:
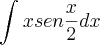
Neste caso posso retirar o 1/2 para fora da integral?

e resolver por partes a partir daí?

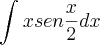


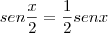



vmouc escreveu:Nesse caso se eu escolher senx/2 como u, como derivo sen x/2?
 e
e 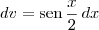 .
.
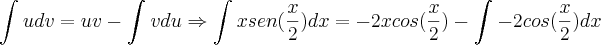

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes

 .
.



