 por carvalhothg » Seg Out 17, 2011 15:41
por carvalhothg » Seg Out 17, 2011 15:41
Dada a função implicita
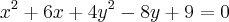
, mostrar que a derivada

no ponto
![P\left[2+\sqrt[]{2},2-\sqrt[]{2} \right] P\left[2+\sqrt[]{2},2-\sqrt[]{2} \right]](/latexrender/pictures/1843017f297bc3d477772eb167272371.png)
é igual a 1/4.
Pessoal eu resolvi este exercício e encontrei:
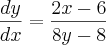
e substitui:
![x=2+\sqrt[]{2} x=2+\sqrt[]{2}](/latexrender/pictures/9d3adf8911b7faedde47dd9cc7a98a26.png)
![y=2-\sqrt[]{2} y=2-\sqrt[]{2}](/latexrender/pictures/87df72083ddcfd529a70b29459bf85ef.png)
Mas só que não encontrei 1/4, alguém pode me ajudar a encontrar meu erro, pois estou tendo dificuldades.
-
carvalhothg
- Usuário Dedicado

-
- Mensagens: 42
- Registrado em: Dom Set 04, 2011 18:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por LuizAquino » Seg Out 17, 2011 17:33
por LuizAquino » Seg Out 17, 2011 17:33
carvalhothg escreveu:Pessoal eu resolvi este exercício e encontrei:
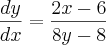
Reveja suas contas, pois essa não é a expressão correta.
Editado pela última vez por
LuizAquino em Seg Out 17, 2011 18:19, em um total de 1 vez.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por carvalhothg » Seg Out 17, 2011 17:57
por carvalhothg » Seg Out 17, 2011 17:57
Realmente eu errei em um sinal no enunciado a expressão correta é:
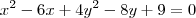
Pois a derivada implicita que eu fiz agora esta correta?
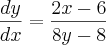
Se não qual seria a derivada implícita correta?
O ponto indicado é este mesmo
![P\left[2+\sqrt[]{2};2-\sqrt[]{2} \right] P\left[2+\sqrt[]{2};2-\sqrt[]{2} \right]](/latexrender/pictures/895f9d23d61de1dfa272c8c7876fd5d5.png)
.
Em suas contas qual seria o valor de dy/dx no ponto acima?
-
carvalhothg
- Usuário Dedicado

-
- Mensagens: 42
- Registrado em: Dom Set 04, 2011 18:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por LuizAquino » Seg Out 17, 2011 18:19
por LuizAquino » Seg Out 17, 2011 18:19
carvalhothg escreveu:Realmente eu errei em um sinal no enunciado a expressão correta é:
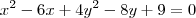
Pois a derivada implicita que eu fiz agora esta correta?
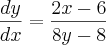
Se não qual seria a derivada implícita correta?
Ainda está errado. O correto para essa nova equação é:
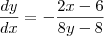
carvalhothg escreveu: ponto indicado é este mesmo
![P\left[2+\sqrt[]{2};2-\sqrt[]{2} \right] P\left[2+\sqrt[]{2};2-\sqrt[]{2} \right]](/latexrender/pictures/895f9d23d61de1dfa272c8c7876fd5d5.png)
.
Em suas contas qual seria o valor de dy/dx no ponto acima?
O valor é 1/4.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivadas] Dificuldade para calcular derivadas CDI 1
por srmai » Seg Nov 04, 2013 01:21
- 0 Respostas
- 2261 Exibições
- Última mensagem por srmai

Seg Nov 04, 2013 01:21
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Interpretação de derivadas e funções
por vinik1 » Qua Out 12, 2011 16:03
- 5 Respostas
- 7472 Exibições
- Última mensagem por vinik1

Qui Out 13, 2011 10:48
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Derivadas em pontos dados
por MarlonMO250 » Sex Mar 01, 2013 21:02
- 6 Respostas
- 4939 Exibições
- Última mensagem por Russman

Sáb Mar 02, 2013 03:42
Cálculo: Limites, Derivadas e Integrais
-
- (derivadas) derivadas com raiz como se faz
por jana garcia » Qua Jun 25, 2014 00:28
- 1 Respostas
- 2963 Exibições
- Última mensagem por e8group

Qua Jun 25, 2014 01:13
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Derivadas com definição de limites
 por concurseironf » Sex Set 05, 2014 18:11
por concurseironf » Sex Set 05, 2014 18:11
- 1 Respostas
- 1992 Exibições
- Última mensagem por DanielFerreira

Dom Set 07, 2014 22:18
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
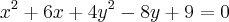 , mostrar que a derivada
, mostrar que a derivada  no ponto
no ponto ![P\left[2+\sqrt[]{2},2-\sqrt[]{2} \right] P\left[2+\sqrt[]{2},2-\sqrt[]{2} \right]](/latexrender/pictures/1843017f297bc3d477772eb167272371.png) é igual a 1/4.
é igual a 1/4.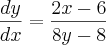
![x=2+\sqrt[]{2} x=2+\sqrt[]{2}](/latexrender/pictures/9d3adf8911b7faedde47dd9cc7a98a26.png)
![y=2-\sqrt[]{2} y=2-\sqrt[]{2}](/latexrender/pictures/87df72083ddcfd529a70b29459bf85ef.png)

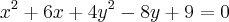 , mostrar que a derivada
, mostrar que a derivada  no ponto
no ponto ![P\left[2+\sqrt[]{2},2-\sqrt[]{2} \right] P\left[2+\sqrt[]{2},2-\sqrt[]{2} \right]](/latexrender/pictures/1843017f297bc3d477772eb167272371.png) é igual a 1/4.
é igual a 1/4.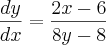
![x=2+\sqrt[]{2} x=2+\sqrt[]{2}](/latexrender/pictures/9d3adf8911b7faedde47dd9cc7a98a26.png)
![y=2-\sqrt[]{2} y=2-\sqrt[]{2}](/latexrender/pictures/87df72083ddcfd529a70b29459bf85ef.png)

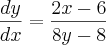

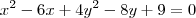
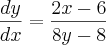
![P\left[2+\sqrt[]{2};2-\sqrt[]{2} \right] P\left[2+\sqrt[]{2};2-\sqrt[]{2} \right]](/latexrender/pictures/895f9d23d61de1dfa272c8c7876fd5d5.png) .
.
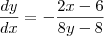
.
