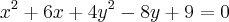 , mostrar que a derivada
, mostrar que a derivada  no ponto
no ponto ![P\left[2+\sqrt[]{2},2-\sqrt[]{2} \right] P\left[2+\sqrt[]{2},2-\sqrt[]{2} \right]](/latexrender/pictures/1843017f297bc3d477772eb167272371.png) é igual a 1/4.
é igual a 1/4.Pessoal eu resolvi este exercício e encontrei:
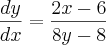
e substitui:
![x=2+\sqrt[]{2} x=2+\sqrt[]{2}](/latexrender/pictures/9d3adf8911b7faedde47dd9cc7a98a26.png)
![y=2-\sqrt[]{2} y=2-\sqrt[]{2}](/latexrender/pictures/87df72083ddcfd529a70b29459bf85ef.png)
Mas só que não encontrei 1/4, alguém pode me ajudar a encontrar meu erro, pois estou tendo dificuldades.

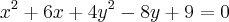 , mostrar que a derivada
, mostrar que a derivada  no ponto
no ponto ![P\left[2+\sqrt[]{2},2-\sqrt[]{2} \right] P\left[2+\sqrt[]{2},2-\sqrt[]{2} \right]](/latexrender/pictures/1843017f297bc3d477772eb167272371.png) é igual a 1/4.
é igual a 1/4.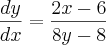
![x=2+\sqrt[]{2} x=2+\sqrt[]{2}](/latexrender/pictures/9d3adf8911b7faedde47dd9cc7a98a26.png)
![y=2-\sqrt[]{2} y=2-\sqrt[]{2}](/latexrender/pictures/87df72083ddcfd529a70b29459bf85ef.png)

carvalhothg escreveu:Pessoal eu resolvi este exercício e encontrei: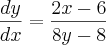

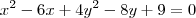
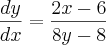
![P\left[2+\sqrt[]{2};2-\sqrt[]{2} \right] P\left[2+\sqrt[]{2};2-\sqrt[]{2} \right]](/latexrender/pictures/895f9d23d61de1dfa272c8c7876fd5d5.png) .
.
carvalhothg escreveu:Realmente eu errei em um sinal no enunciado a expressão correta é:
Pois a derivada implicita que eu fiz agora esta correta?
Se não qual seria a derivada implícita correta?
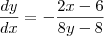
carvalhothg escreveu: ponto indicado é este mesmo.
Em suas contas qual seria o valor de dy/dx no ponto acima?

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)