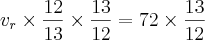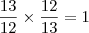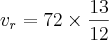por BiiaSweet » Sex Out 14, 2011 17:47
por BiiaSweet » Sex Out 14, 2011 17:47
Oi.
O exercicio que estou resolvendo tem os seguintes pontos importantes:
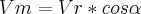
Eu sei que a
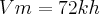
E que o
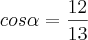
A minha dificuldade esta em algo simples, sempre me compliquei ao ter que resolver equações como esta:
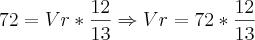
Não consigo resolver =T alguém pode me explicar como e faço esses cálculos simples?
Obrigada! ^^
-
BiiaSweet
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sex Out 14, 2011 17:30
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Curso Técnico em Bioquimica
- Andamento: formado
 por TheoFerraz » Sex Out 14, 2011 18:32
por TheoFerraz » Sex Out 14, 2011 18:32
Parece-me que sua duvida nao é nem de trigonometria, não é ? =P
se eu entendi bem voce quer resolver a equação
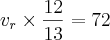
simplesmente ?
Explicando porcamente eu diria que voce deve "passar a fração para o outro lado, invertendo-a". e é maomeno isso mesmo. mas vou explicar melhor o por que:
temos isso :
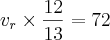
voce concorda que uma equação, assim como uma balança pode ser modificada IGUALMENTE dos dois lados sem que a igualdade seja violada ?
então vamos multiplicar ambos os lados da equação pela fração inversa à essa! por que ? simplesmente por que quando eu fizer

resultará em 1 e todo numero multiplicado a um é ele mesmo! observe :
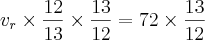
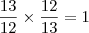
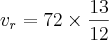
-
TheoFerraz
- Colaborador Voluntário

-
- Mensagens: 107
- Registrado em: Qua Abr 13, 2011 19:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Física
- Andamento: cursando
 por TheoFerraz » Sex Out 14, 2011 18:35
por TheoFerraz » Sex Out 14, 2011 18:35
Para simplificar voce pode pensar em passar a fração invertida.
Ou melhor... sempre que houver algo multiplicando todo um lado da igualdade, voce pode passa-lo para o outro dividindo todo o outro lado.
E a operação inversa é válida também.
Nao sei se era isso. espero ter ajudado.
-
TheoFerraz
- Colaborador Voluntário

-
- Mensagens: 107
- Registrado em: Qua Abr 13, 2011 19:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Física
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Multiplicação
por Guga1981 » Qua Fev 11, 2015 16:25
- 0 Respostas
- 1336 Exibições
- Última mensagem por Guga1981

Qua Fev 11, 2015 16:25
Conjuntos
-
- Multiplicação por -1
por Luan_Santyago » Qui Mar 26, 2015 17:04
- 1 Respostas
- 1512 Exibições
- Última mensagem por Russman

Sáb Mar 28, 2015 02:37
Funções
-
- Multiplicação de polinômios
por Lolozita » Ter Jun 23, 2009 20:54
- 1 Respostas
- 3035 Exibições
- Última mensagem por marciommuniz

Ter Jun 23, 2009 23:16
Polinômios
-
- Multiplicação de raiz
por lordkot » Ter Abr 17, 2012 18:02
- 3 Respostas
- 2522 Exibições
- Última mensagem por DanielFerreira

Ter Abr 24, 2012 20:18
Álgebra Elementar
-
- Multiplicação de cossenos
por anfran1 » Sex Jun 29, 2012 10:39
- 5 Respostas
- 5168 Exibições
- Última mensagem por Arkanus Darondra

Dom Jul 01, 2012 12:48
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
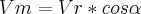
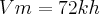
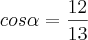
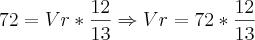


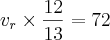 simplesmente ?
simplesmente ? resultará em 1 e todo numero multiplicado a um é ele mesmo! observe :
resultará em 1 e todo numero multiplicado a um é ele mesmo! observe :