 por beel » Ter Out 04, 2011 23:44
por beel » Ter Out 04, 2011 23:44
Como achar o valor de (fog)'(x) para as funções f,g e o ponto x dado que
f(u)= 1 - 1/u , u=g(x)=1/(1-x) e x=-1 ?
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por LuizAquino » Qua Out 05, 2011 10:57
por LuizAquino » Qua Out 05, 2011 10:57
isanobile escreveu:Como achar o valor de (fog)'(x) para as funções f,g e o ponto x dado (...)
Primeiro, lembre-se que escrever

é o mesmo que escrever
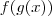
. Sendo assim, calcular
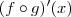
é o mesmo que calcular
![[f(g(x))]^\prime [f(g(x))]^\prime](/latexrender/pictures/f618369117b4e2d375770b45645fdbfe.png)
. Basta então aplicar a Regra da Cadeia:
![[f(g(x))]^\prime = f^\prime(g(x))g^\prime(x) [f(g(x))]^\prime = f^\prime(g(x))g^\prime(x)](/latexrender/pictures/43b700ef86b2f826eb9f4de60fe885f5.png)
Já que

e

, você sabe que

e
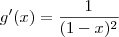
.
Fazendo a composição de
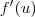
com

, temos que
![f^\prime(g(x)) = \frac{1}{[g(x)]^2} = (1-x)^2 f^\prime(g(x)) = \frac{1}{[g(x)]^2} = (1-x)^2](/latexrender/pictures/f403bf60f9c98ad5c5814948f3960f99.png)
.
Agora tente continuar a resolução substituindo essas informações na expressão obtida pela Regra da Cadeia.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por beel » Sex Out 07, 2011 21:26
por beel » Sex Out 07, 2011 21:26
Seria
![(1-x)^2[\frac{1}{(1-x)^2]} (1-x)^2[\frac{1}{(1-x)^2]}](/latexrender/pictures/176447d5c7aa1fe81df00700d1de4005.png)
?
[ f'(g(x))g'(x) ]
E como no enunciado ele fala que x=-1 é so substituir?
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por LuizAquino » Sáb Out 08, 2011 18:30
por LuizAquino » Sáb Out 08, 2011 18:30
isanobile escreveu:Seria
![(1-x)^2\left[\frac{1}{(1-x)^2}\right] (1-x)^2\left[\frac{1}{(1-x)^2}\right]](/latexrender/pictures/31b13fccba626b705695f23b6c3978cc.png)
?
[ f'(g(x))g'(x) ]
Sim. Mas lembrando-se que x = 1 não faz parte do domínio de g, podemos escrever que:
![[f(g(x))]^\prime = (1-x)^2 \cdot \frac{1}{(1-x)^2} = 1 [f(g(x))]^\prime = (1-x)^2 \cdot \frac{1}{(1-x)^2} = 1](/latexrender/pictures/2e93e5ec05b749b422a245d2bd1704fc.png)
isanobile escreveu:E como no enunciado ele fala que x=-1 é so substituir?
Sim. Mas como a função derivada é constante, o seu valor em x = -1 (ou em qualquer outro ponto de seu domínio) é simplesmente 1. Isto é, temos que
![[f(g(-1))]^\prime = 1 [f(g(-1))]^\prime = 1](/latexrender/pictures/5aeeb806f130239d749166c3fa28d436.png)
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por beel » Qui Out 13, 2011 12:31
por beel » Qui Out 13, 2011 12:31
Entendi, obrigada.
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [CALCULO] derivada de função composta
por beel » Ter Out 04, 2011 22:45
- 4 Respostas
- 2229 Exibições
- Última mensagem por beel

Dom Out 16, 2011 16:55
Cálculo: Limites, Derivadas e Integrais
-
- [CALCULO] derivada de função composta 2
por beel » Ter Out 04, 2011 22:58
- 5 Respostas
- 3116 Exibições
- Última mensagem por beel

Qui Out 13, 2011 12:33
Cálculo: Limites, Derivadas e Integrais
-
- [Função composta]Achar o dominio de uma função composta
por lucasmath » Dom Abr 12, 2015 16:09
- 0 Respostas
- 2229 Exibições
- Última mensagem por lucasmath

Dom Abr 12, 2015 16:09
Funções
-
- [FUNÇÃO] NAO CONSIGO ENTENDER FUNÇÃO COMPOSTA!
por Gabriela AlmeidaS » Seg Mai 12, 2014 19:18
- 5 Respostas
- 5452 Exibições
- Última mensagem por Toussantt

Dom Jan 24, 2016 15:34
Funções
-
- Função composta
por scorpion » Sáb Out 25, 2008 11:09
- 2 Respostas
- 4197 Exibições
- Última mensagem por scorpion

Qua Out 29, 2008 14:26
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 é o mesmo que escrever
é o mesmo que escrever 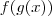 . Sendo assim, calcular
. Sendo assim, calcular 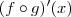 é o mesmo que calcular
é o mesmo que calcular ![[f(g(x))]^\prime [f(g(x))]^\prime](/latexrender/pictures/f618369117b4e2d375770b45645fdbfe.png) . Basta então aplicar a Regra da Cadeia:
. Basta então aplicar a Regra da Cadeia:![[f(g(x))]^\prime = f^\prime(g(x))g^\prime(x) [f(g(x))]^\prime = f^\prime(g(x))g^\prime(x)](/latexrender/pictures/43b700ef86b2f826eb9f4de60fe885f5.png)
 e
e  , você sabe que
, você sabe que  e
e 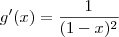 .
.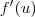 com
com  , temos que
, temos que ![f^\prime(g(x)) = \frac{1}{[g(x)]^2} = (1-x)^2 f^\prime(g(x)) = \frac{1}{[g(x)]^2} = (1-x)^2](/latexrender/pictures/f403bf60f9c98ad5c5814948f3960f99.png) .
.
![(1-x)^2[\frac{1}{(1-x)^2]} (1-x)^2[\frac{1}{(1-x)^2]}](/latexrender/pictures/176447d5c7aa1fe81df00700d1de4005.png) ?
?
?
![[f(g(x))]^\prime = (1-x)^2 \cdot \frac{1}{(1-x)^2} = 1 [f(g(x))]^\prime = (1-x)^2 \cdot \frac{1}{(1-x)^2} = 1](/latexrender/pictures/2e93e5ec05b749b422a245d2bd1704fc.png)
![[f(g(-1))]^\prime = 1 [f(g(-1))]^\prime = 1](/latexrender/pictures/5aeeb806f130239d749166c3fa28d436.png) .
.
