 por teteffs » Qui Out 06, 2011 17:32
por teteffs » Qui Out 06, 2011 17:32
Boa tarde pessoal ,curso Engenharia de Produção e estou com uma dúvida quanto a uma questão de calculo de volume de um solido por integral definida.Estou em duvida quanto ao raio do grafico. A questão é a seguinte: A região R, limitada pela curva y=1/4 x², o eixo x e as retas x=1 e x=4 gira em torno do eixo x. Encontrar o volume do sólido de revolução gerado.
Bom primeiramente eu procurei o xv que é xv=0 ja que em 1/4 x², o xv sendo -b/2a e nao havendo o termo b o resultado é 0. A partir disso em minha tabela de valores de x e y ficaria: Lembrando o xv deu zero entao conto 2 valores antes do zero e 2 valores depois do zero para minha tabela
x y
-2 1 Bom pessoal quando fiz o grafico que resulta em duas parábolas,uma concavidade para cima e a outra para baixo, mas estou em duvida qual sera
-1 1/4 o raio,sei que é algum y,o grafico demonstra isso, mas quando se faz o grafico os valores vao de 0 a 2 ,e ele quer de 1 a 4 portanto creio que o raio
0 0 nao sera somente o y,alguem pode me ajudar a pensar?
1 1/4
2 1
Amanda Teff
-
teteffs
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qui Out 06, 2011 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produçao
- Andamento: cursando
 por LuizAquino » Qui Out 06, 2011 18:43
por LuizAquino » Qui Out 06, 2011 18:43
teteffs escreveu:A região R, limitada pela curva y=1/4 x², o eixo x e as retas x=1 e x=4 gira em torno do eixo x. Encontrar o volume do sólido de revolução gerado.
A figura abaixo ilustra a região e o sólido gerado.
Note que cada seção transversal, perpendicular ao eixo x, será um círculo de raio y (sendo que
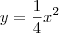
). Portanto, a área de cada seção será dada por:
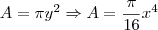
Enxergando a área A como uma função de x, o volume desse sólido será dado por
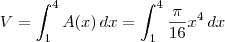
Agora tente terminar o exercício.
ObservaçãoSe deseja revisar esse conteúdo, então eu recomendo a vídeo-aula "38. Cálculo I - Aplicação de Integrais no Cálculo de Volumes". Ela está disponível em meu canal no YouTube:
http://www.youtube.com/LCMAquino
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por teteffs » Sex Out 07, 2011 17:53
por teteffs » Sex Out 07, 2011 17:53
Oi Luiz Aquino mto obrigado pela ajuda entao eu havia pensado como vc e achei este resultado:
CodeCogsEqn.gif
Bom eu nao vejo uma outra maneira de achar o raio a nao ser aquele mas meus colegas de faculdade teimam em dizer q esta errado, que o professor nao concorda!!!
Amanda Teff
-
teteffs
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qui Out 06, 2011 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produçao
- Andamento: cursando
 por teteffs » Sex Out 07, 2011 17:56
por teteffs » Sex Out 07, 2011 17:56
teteffs escreveu:Oi Luiz Aquino mto obrigado pela ajuda entao eu havia pensado como vc e achei este resultado:
Bom eu nao vejo uma outra maneira de achar o raio a nao ser aquele mas meus colegas de faculdade teimam em dizer q esta errado, que o professor nao concorda!!!
- Anexos
-
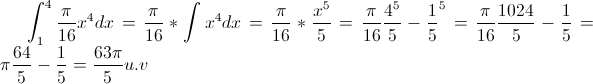
- CodeCogsEqn.gif (2.92 KiB) Exibido 6694 vezes
Amanda Teff
-
teteffs
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qui Out 06, 2011 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produçao
- Andamento: cursando
 por LuizAquino » Sex Out 07, 2011 19:11
por LuizAquino » Sex Out 07, 2011 19:11
A solução correta é:
![V = \int_1^4 \frac{\pi}{16} x^4 \, dx = \left[\frac{\pi}{80}x^5\right]_1^4 = \frac{\pi}{80}\cdot 4^5 - \frac{\pi}{80}\cdot 1^5 = \frac{1023}{80}\pi\textrm{ (u. v. - unidade de volume)} V = \int_1^4 \frac{\pi}{16} x^4 \, dx = \left[\frac{\pi}{80}x^5\right]_1^4 = \frac{\pi}{80}\cdot 4^5 - \frac{\pi}{80}\cdot 1^5 = \frac{1023}{80}\pi\textrm{ (u. v. - unidade de volume)}](/latexrender/pictures/69c7666f93f10d57639ba2187096737f.png) Observação
ObservaçãoVeja na figura abaixo que dado um número x no intervalo [1, 4], o valor de y associado a ele (através da curva
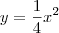
) será o raio do círculo que representa uma seção transversal do sólido.
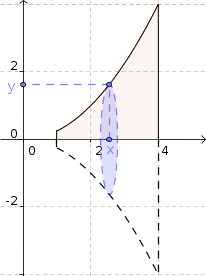
- regiãoR-raio-y.png (81.98 KiB) Exibido 6688 vezes
Editado pela última vez por
LuizAquino em Sex Out 07, 2011 19:28, em um total de 1 vez.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por teteffs » Sex Out 07, 2011 19:20
por teteffs » Sex Out 07, 2011 19:20
[quote="LuizAquino"]A solução correta é:
Oiiii então Luis Aquino essa questão é de uma prova que tive,todo mundo da sala errou sabe,muitos fizeram a questao inclusive eu na prova,e o raciocinio era o mesmo que o seu, havia dado este mesmo resultado seu,so que o professor deu a questao que vc resolveu como errada,por isso calculei dessa outra maneira,ele pediu entao q refizessemos essa questao valendo nota,e por isso ainda nao corrigiu a questao,nao entendemos pq p gente dava esse valor seu mesmo mas cmo ele ja deu como errado estamos ficando doidos.
Amanda Teff
-
teteffs
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qui Out 06, 2011 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produçao
- Andamento: cursando
 por LuizAquino » Sáb Out 08, 2011 19:40
por LuizAquino » Sáb Out 08, 2011 19:40
Se o enunciado do exercício é exatamente como o que você postou, então a resposta correta é como indiquei nas mensagens anteriores.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por teteffs » Sáb Out 08, 2011 20:18
por teteffs » Sáb Out 08, 2011 20:18
LuizAquino escreveu:Se o enunciado do exercício é exatamente como o que você postou, então a resposta correta é como indiquei nas mensagens anteriores.
O enunciado é aquele mesmo,muitissimo obrigado pela ajuda e paciencia, tenha um bom fim de semana,fique com Deus!
Amanda Teff
-
teteffs
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qui Out 06, 2011 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produçao
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [calculo] integral definida
por beel » Sex Nov 18, 2011 12:29
- 1 Respostas
- 1839 Exibições
- Última mensagem por LuizAquino

Sex Nov 18, 2011 22:05
Cálculo: Limites, Derivadas e Integrais
-
- [calculo] integral definida
por beel » Sex Nov 18, 2011 12:48
- 1 Respostas
- 1979 Exibições
- Última mensagem por LuizAquino

Sex Nov 18, 2011 22:07
Cálculo: Limites, Derivadas e Integrais
-
- [calculo] integral definida
por beel » Sex Nov 18, 2011 12:53
- 1 Respostas
- 2017 Exibições
- Última mensagem por LuizAquino

Sex Nov 18, 2011 22:00
Cálculo: Limites, Derivadas e Integrais
-
- [calculo] integral definida
por beel » Sex Nov 18, 2011 13:29
- 1 Respostas
- 1722 Exibições
- Última mensagem por MarceloFantini

Sex Nov 18, 2011 16:18
Cálculo: Limites, Derivadas e Integrais
-
- Calculo de Integral definida..
por Nei Stolberg » Qui Mar 21, 2019 19:11
- 0 Respostas
- 4727 Exibições
- Última mensagem por Nei Stolberg

Qui Mar 21, 2019 19:11
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


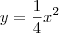 ). Portanto, a área de cada seção será dada por:
). Portanto, a área de cada seção será dada por: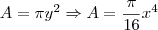
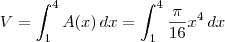

![V = \int_1^4 \frac{\pi}{16} x^4 \, dx = \left[\frac{\pi}{80}x^5\right]_1^4 = \frac{\pi}{80}\cdot 4^5 - \frac{\pi}{80}\cdot 1^5 = \frac{1023}{80}\pi\textrm{ (u. v. - unidade de volume)} V = \int_1^4 \frac{\pi}{16} x^4 \, dx = \left[\frac{\pi}{80}x^5\right]_1^4 = \frac{\pi}{80}\cdot 4^5 - \frac{\pi}{80}\cdot 1^5 = \frac{1023}{80}\pi\textrm{ (u. v. - unidade de volume)}](/latexrender/pictures/69c7666f93f10d57639ba2187096737f.png)
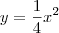 ) será o raio do círculo que representa uma seção transversal do sólido.
) será o raio do círculo que representa uma seção transversal do sólido.