Boa tarde pessoal ,curso Engenharia de Produção e estou com uma dúvida quanto a uma questão de calculo de volume de um solido por integral definida.Estou em duvida quanto ao raio do grafico. A questão é a seguinte: A região R, limitada pela curva y=1/4 x², o eixo x e as retas x=1 e x=4 gira em torno do eixo x. Encontrar o volume do sólido de revolução gerado.
Bom primeiramente eu procurei o xv que é xv=0 ja que em 1/4 x², o xv sendo -b/2a e nao havendo o termo b o resultado é 0. A partir disso em minha tabela de valores de x e y ficaria: Lembrando o xv deu zero entao conto 2 valores antes do zero e 2 valores depois do zero para minha tabela
x y
-2 1 Bom pessoal quando fiz o grafico que resulta em duas parábolas,uma concavidade para cima e a outra para baixo, mas estou em duvida qual sera
-1 1/4 o raio,sei que é algum y,o grafico demonstra isso, mas quando se faz o grafico os valores vao de 0 a 2 ,e ele quer de 1 a 4 portanto creio que o raio
0 0 nao sera somente o y,alguem pode me ajudar a pensar?
1 1/4
2 1
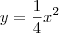). Portanto, a área de cada seção será dada por: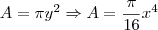
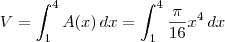
![V = \int_1^4 \frac{\pi}{16} x^4 \, dx = \left[\frac{\pi}{80}x^5\right]_1^4 = \frac{\pi}{80}\cdot 4^5 - \frac{\pi}{80}\cdot 1^5 = \frac{1023}{80}\pi\textrm{ (u. v. - unidade de volume)}](/latexrender/pictures/69c7666f93f10d57639ba2187096737f.png "V = \int_1^4 \frac{\pi}{16} x^4 \, dx = \left[\frac{\pi}{80}x^5\right]_1^4 = \frac{\pi}{80}\cdot 4^5 - \frac{\pi}{80}\cdot 1^5 = \frac{1023}{80}\pi\textrm{ (u. v. - unidade de volume)}")
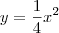) será o raio do círculo que representa uma seção transversal do sólido.![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)