 por moyses » Qui Out 06, 2011 12:16
por moyses » Qui Out 06, 2011 12:16
Bom pessoal tenho uma duvida nesse limite aqui:
![\lim_{x\rightarrow1}\frac{\sqrt[5]{x}-\sqrt[3]{x}}{x-1} \lim_{x\rightarrow1}\frac{\sqrt[5]{x}-\sqrt[3]{x}}{x-1}](/latexrender/pictures/00a53dd977ca00c549bb7b8dbe5fab6b.png)
a minha duvida é de como eu faço ao conjugado disso. sem usar derivada pois eu aindo vou aprender isso

.
-
moyses
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Seg Ago 29, 2011 09:55
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: SISTEMA DE INFORMAÇÃO
- Andamento: cursando
 por Claudin » Qui Out 06, 2011 14:10
por Claudin » Qui Out 06, 2011 14:10
Tem certeza que o limite é este?
Ou é assim?
![\lim_{x\rightarrow{1}}\frac{\sqrt[3]{x}-\sqrt[3]{x}}{x-1} \lim_{x\rightarrow{1}}\frac{\sqrt[3]{x}-\sqrt[3]{x}}{x-1}](/latexrender/pictures/d7874cbfc35959bb33386639997b65db.png)
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por moyses » Qui Out 06, 2011 15:39
por moyses » Qui Out 06, 2011 15:39
sim cara esse é o limite do jeito que você esta vendo ai. e isso mesmo

-
moyses
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Seg Ago 29, 2011 09:55
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: SISTEMA DE INFORMAÇÃO
- Andamento: cursando
 por LuizAquino » Qui Out 06, 2011 18:11
por LuizAquino » Qui Out 06, 2011 18:11
moyses escreveu:Bom pessoal tenho uma duvida nesse limite aqui:
![\lim_{x\to 1}\frac{\sqrt[5]{x}-\sqrt[3]{x}}{x-1} \lim_{x\to 1}\frac{\sqrt[5]{x}-\sqrt[3]{x}}{x-1}](/latexrender/pictures/1951b4d5480ec962426ffbd7942ce870.png)
Faça a substituição

. Com isso, quando x tende para 1, temos que u também tende para 1. Além disso, podemos escrever que:
![\lim_{x\to 1}\frac{\sqrt[5]{x}-\sqrt[3]{x}}{x-1} = \lim_{u\to 1}\frac{u^3 - u^5}{u^{15}-1} = \lim_{u\to 1}\frac{u^3\left(1 - u^2\right)}{u^{15}-1} \lim_{x\to 1}\frac{\sqrt[5]{x}-\sqrt[3]{x}}{x-1} = \lim_{u\to 1}\frac{u^3 - u^5}{u^{15}-1} = \lim_{u\to 1}\frac{u^3\left(1 - u^2\right)}{u^{15}-1}](/latexrender/pictures/91ad548d3af122966e5b38ab3399694f.png)
Agora tente terminar o exercício.
ObservaçãoEditado após o comentário abaixo.
Re: Limites, conjugado de raizesviewtopic.php?p=21429#p21445Editado pela última vez por
LuizAquino em Sex Out 07, 2011 08:33, em um total de 6 vezes.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por moyses » Qui Out 06, 2011 18:50
por moyses » Qui Out 06, 2011 18:50
como assim não entendi o que você fez exatamente?
-
moyses
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Seg Ago 29, 2011 09:55
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: SISTEMA DE INFORMAÇÃO
- Andamento: cursando
 por Claudin » Qui Out 06, 2011 20:40
por Claudin » Qui Out 06, 2011 20:40
Ele atribuiu

, pois seria divisível por 3 e 5.
Detalhando para o entendimentoSendo assim ficaria:
![\sqrt[5]{u^{15}}\Rightarrow u^\frac{15}{5}= u^3 \sqrt[5]{u^{15}}\Rightarrow u^\frac{15}{5}= u^3](/latexrender/pictures/162aeda40d0a3311ed9cde7b0affcc09.png)
![\sqrt[3]{u^{15}}\Rightarrow u^\frac{15}{3}= u^5 \sqrt[3]{u^{15}}\Rightarrow u^\frac{15}{3}= u^5](/latexrender/pictures/12cea3cbb416a435cbe3561b9ac06d01.png) Obs:
Obs: Quando eu fui Colaborador oficial do fórum, tinha como ideal sempre nas discussões da sala fechada o detalhamento das questões, pois no meu entendimento a matemática se aprende praticando, e as vezes a pessoa martela, martela em exercício e não sai nada, talvez a saída seja estudar por uma resolução detalhada. Bom essa é minha opinião.
Valeu pela dica Luiz.
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Qui Out 06, 2011 21:07
por LuizAquino » Qui Out 06, 2011 21:07
moyses escreveu:como assim não entendi o que você fez exatamente?
Eu fiz uma substituição de variável para simplificar a expressão que aparece no limite.
A escolha de

foi realizada para simplificar os radicais existentes.
Claudin escreveu:Ele atribuiu

, pois seria divisível por 3 e 5.
Deixando claro: o número 15 para a
potência foi escolhido pois
ele é divisível por 3 e 5 (que são os índices aparecendo nas raízes). Da forma que você escreveu, parece que está sendo afirmado que
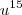
é divisível por 3 e 5, o que não faz sentido nesse contexto.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por moyses » Qui Out 06, 2011 23:01
por moyses » Qui Out 06, 2011 23:01
valew cara muioto obrigado!
-
moyses
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Seg Ago 29, 2011 09:55
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: SISTEMA DE INFORMAÇÃO
- Andamento: cursando
 por LuizAquino » Sex Out 07, 2011 11:04
por LuizAquino » Sex Out 07, 2011 11:04
moyses escreveu:(...) por que embaixo você colocou x igual a u , sendo que x que você falou era u elevado a 15?
Eu editei a mensagem acima após seu comentário. De fato, tinha faltado substituir x por
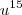
no denominador.
Para continuar a resolução, aqui vai outra dica: divida o numerador e o denominador por

. Se você não se recorda como efetuar a divisão entre polinômios, eu recomendo que você assista as vídeo-aulas:
#9 Polinômios Divisão Método das Chaveshttp://www.youtube.com/watch?v=FDqhD7ADd1s#12 Polinômios Divisão Dispositivo Briot Rufffinihttp://www.youtube.com/watch?v=YhDJ8SahIQQClaudin escreveu:Obs: Quando eu fui Colaborador oficial do fórum, tinha como ideal sempre nas discussões da sala fechada o detalhamento das questões, pois no meu entendimento a matemática se aprende praticando, e as vezes a pessoa martela, martela em exercício e não sai nada, talvez a saída seja estudar por uma resolução detalhada. Bom essa é minha opinião.
Você já deve ter percebido que em todos os bons livros de Cálculo (e das outras disciplinas de Matemática), os exemplos geralmente
não são 100% detalhados. Os autores tipicamente "pulam" alguns passos na resolução. Isso é feito de propósito. O
leitor deve ser capaz de "preencher" os passos que faltam. É aquela velha história: o professor indica o caminho, mas é o aluno quem deve percorrê-lo.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por moyses » Sex Out 07, 2011 11:30
por moyses » Sex Out 07, 2011 11:30
Valeww professor luiz , valew claudin pelos seus comentarios e ajudas . Muito obirgado. SÓ uma pergunta para aprender limites trigonométricos que livro você recomenda ou videos na internet, sei la muito obriogado de novo.
-
moyses
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Seg Ago 29, 2011 09:55
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: SISTEMA DE INFORMAÇÃO
- Andamento: cursando
 por LuizAquino » Sáb Out 08, 2011 20:50
por LuizAquino » Sáb Out 08, 2011 20:50
moyses escreveu:(...)
Só uma pergunta para aprender limites trigonométricos que livro você recomenda ou videos na internet
(...)
Basta consultar o livro de Cálculo que você melhor se identificar. Não há uma "receita pronta" que sirva para todas as pessoas.
Quanto a um vídeo, há disponível em meu
canal no YouTube a vídeo-aula "07. Cálculo I - Limites Trigonométricos".
Com certeza fazendo uma busca no YouTube você deve encontrar vídeos de outras pessoas abordando esse assunto.
De qualquer modo, vale destacar o seguinte: se você não dominar o conteúdo de trigonometria abordado no ensino médio, então será difícil você conseguir resolver limites trigonométricos. Por isso, uma revisão desse conteúdo é fortemente recomendado.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por moyses » Sáb Out 08, 2011 21:45
por moyses » Sáb Out 08, 2011 21:45
gente eu não consigui dividir astrves do metodo da chaves nem pelo metodo de briout ruffini. alguem poderia me ajudar é só a parte debaixo o denominador

não teria como fatorar? sei la pelo método de divisão fica muito grande , e ainda sobra resto. desde já agradeço a atenção de vocês.
-
moyses
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Seg Ago 29, 2011 09:55
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: SISTEMA DE INFORMAÇÃO
- Andamento: cursando
 por LuizAquino » Dom Out 09, 2011 08:26
por LuizAquino » Dom Out 09, 2011 08:26
moyses escreveu:gente eu não consegui dividir através do método da chaves nem pelo método de briout ruffini.
(...)
sei la pelo método de divisão fica muito grande , e ainda sobra resto.
Não desanime! O resultado dessa divisão é grande mesmo! Entretanto não há resto.
Refaça as suas contas. O que você deve obter no final é:
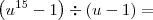

-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por moyses » Dom Out 09, 2011 11:59
por moyses » Dom Out 09, 2011 11:59
mais e agora é só isso, professor luiz. puxa que conta grande, pelo que eu percebi ta somando. e a parte de cima o limite da parte de cima ta tendendo a 0, tem como simplificar isso?

=

mais e agora como simplificar , tem como? ou o limite vai dar 0 ?
-
moyses
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Seg Ago 29, 2011 09:55
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: SISTEMA DE INFORMAÇÃO
- Andamento: cursando
 por LuizAquino » Dom Out 09, 2011 12:34
por LuizAquino » Dom Out 09, 2011 12:34
moyses escreveu:(...) mais e agora como simplificar , tem como? (...)
Você já sabe que:

Sendo assim, você pode afirmar que:
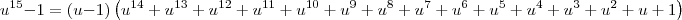
Usando essa informação, note que:



Agora tente continuar.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por moyses » Dom Out 09, 2011 17:04
por moyses » Dom Out 09, 2011 17:04
agora ta facil! to fazendo aqui , mais uma duvida e esse

no denominador, você colocou porque ?
-
moyses
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Seg Ago 29, 2011 09:55
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: SISTEMA DE INFORMAÇÃO
- Andamento: cursando
 por moyses » Dom Out 09, 2011 17:15
por moyses » Dom Out 09, 2011 17:15
ahh ta mancada MINHA

,

eu entendi você igualou a divisão de u elevado a 15 / u-1 e o resultado . ai voce passou o divisor para outro lado multiplicando, ae assim ! não é a toa que você deve ser chamado de Professor parabens cara! Só para entender antes eu tinha o limite original, depois você me mostrou que alguns casos tem que mudar a varivel x para outra neste caso o u elevado a 15. eu tabem queria saber qunado eu preciso mudar a variavel do limite? desde ja muito obrigado rsrsrs, valeww mesmo cara,valeww tabem claudin!
-
moyses
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Seg Ago 29, 2011 09:55
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: SISTEMA DE INFORMAÇÃO
- Andamento: cursando
 por LuizAquino » Dom Out 09, 2011 19:16
por LuizAquino » Dom Out 09, 2011 19:16
moyses escreveu:Só para entender antes eu tinha o limite original, depois você me mostrou que alguns casos tem que mudar a varivel x para outra neste caso o u elevado a 15. eu tabem queria saber qunado eu preciso mudar a variavel do limite?
Tipicamente você irá efetuar uma substituição de variável quando quiser simplificar a expressão de um limite, de modo que o nova expressão fique mais próxima de limites já conhecidos.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [LIMITES] Limites com duas raízes
por Atom » Dom Mai 25, 2014 20:22
- 1 Respostas
- 2059 Exibições
- Última mensagem por e8group

Dom Mai 25, 2014 21:59
Cálculo: Limites, Derivadas e Integrais
-
- Problema com raízes dos limites
por Ademir Jose » Sex Mar 09, 2012 21:45
- 5 Respostas
- 3071 Exibições
- Última mensagem por Ademir Jose

Dom Mar 11, 2012 19:14
Cálculo: Limites, Derivadas e Integrais
-
- Limites com Raízes Cúbicas
por nathilopes » Qua Mar 05, 2014 02:23
- 2 Respostas
- 2910 Exibições
- Última mensagem por nathilopes

Qua Mar 05, 2014 16:09
Cálculo: Limites, Derivadas e Integrais
-
- [limites] Dificuldade com raízes
por baloso » Sex Abr 25, 2014 19:22
- 2 Respostas
- 2046 Exibições
- Última mensagem por baloso

Seg Abr 28, 2014 19:33
Cálculo: Limites, Derivadas e Integrais
-
- Ajuda, Limites com Raizes
por rodrigojuara » Ter Mar 10, 2015 22:39
- 1 Respostas
- 1177 Exibições
- Última mensagem por adauto martins

Qua Mar 11, 2015 13:21
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x\rightarrow1}\frac{\sqrt[5]{x}-\sqrt[3]{x}}{x-1} \lim_{x\rightarrow1}\frac{\sqrt[5]{x}-\sqrt[3]{x}}{x-1}](/latexrender/pictures/00a53dd977ca00c549bb7b8dbe5fab6b.png) a minha duvida é de como eu faço ao conjugado disso. sem usar derivada pois eu aindo vou aprender isso
a minha duvida é de como eu faço ao conjugado disso. sem usar derivada pois eu aindo vou aprender isso  .
.
![\lim_{x\rightarrow1}\frac{\sqrt[5]{x}-\sqrt[3]{x}}{x-1} \lim_{x\rightarrow1}\frac{\sqrt[5]{x}-\sqrt[3]{x}}{x-1}](/latexrender/pictures/00a53dd977ca00c549bb7b8dbe5fab6b.png) a minha duvida é de como eu faço ao conjugado disso. sem usar derivada pois eu aindo vou aprender isso
a minha duvida é de como eu faço ao conjugado disso. sem usar derivada pois eu aindo vou aprender isso  .
.
![\lim_{x\rightarrow{1}}\frac{\sqrt[3]{x}-\sqrt[3]{x}}{x-1} \lim_{x\rightarrow{1}}\frac{\sqrt[3]{x}-\sqrt[3]{x}}{x-1}](/latexrender/pictures/d7874cbfc35959bb33386639997b65db.png)






 . Com isso, quando x tende para 1, temos que u também tende para 1. Além disso, podemos escrever que:
. Com isso, quando x tende para 1, temos que u também tende para 1. Além disso, podemos escrever que:![\lim_{x\to 1}\frac{\sqrt[5]{x}-\sqrt[3]{x}}{x-1} = \lim_{u\to 1}\frac{u^3 - u^5}{u^{15}-1} = \lim_{u\to 1}\frac{u^3\left(1 - u^2\right)}{u^{15}-1} \lim_{x\to 1}\frac{\sqrt[5]{x}-\sqrt[3]{x}}{x-1} = \lim_{u\to 1}\frac{u^3 - u^5}{u^{15}-1} = \lim_{u\to 1}\frac{u^3\left(1 - u^2\right)}{u^{15}-1}](/latexrender/pictures/91ad548d3af122966e5b38ab3399694f.png)


 , pois seria divisível por 3 e 5.
, pois seria divisível por 3 e 5.![\sqrt[5]{u^{15}}\Rightarrow u^\frac{15}{5}= u^3 \sqrt[5]{u^{15}}\Rightarrow u^\frac{15}{5}= u^3](/latexrender/pictures/162aeda40d0a3311ed9cde7b0affcc09.png)
![\sqrt[3]{u^{15}}\Rightarrow u^\frac{15}{3}= u^5 \sqrt[3]{u^{15}}\Rightarrow u^\frac{15}{3}= u^5](/latexrender/pictures/12cea3cbb416a435cbe3561b9ac06d01.png)

 foi realizada para simplificar os radicais existentes.
foi realizada para simplificar os radicais existentes., pois seria divisível por 3 e 5.
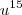 é divisível por 3 e 5, o que não faz sentido nesse contexto.
é divisível por 3 e 5, o que não faz sentido nesse contexto.

 !
! 

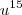 no denominador.
no denominador. . Se você não se recorda como efetuar a divisão entre polinômios, eu recomendo que você assista as vídeo-aulas:
. Se você não se recorda como efetuar a divisão entre polinômios, eu recomendo que você assista as vídeo-aulas:


 não teria como fatorar? sei la pelo método de divisão fica muito grande , e ainda sobra resto. desde já agradeço a atenção de vocês.
não teria como fatorar? sei la pelo método de divisão fica muito grande , e ainda sobra resto. desde já agradeço a atenção de vocês.
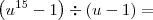


 =
=  mais e agora como simplificar , tem como? ou o limite vai dar 0 ?
mais e agora como simplificar , tem como? ou o limite vai dar 0 ?

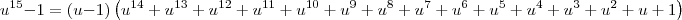




 no denominador, você colocou porque ?
no denominador, você colocou porque ?
 ,
,  eu entendi você igualou a divisão de u elevado a 15 / u-1 e o resultado . ai voce passou o divisor para outro lado multiplicando, ae assim ! não é a toa que você deve ser chamado de Professor parabens cara! Só para entender antes eu tinha o limite original, depois você me mostrou que alguns casos tem que mudar a varivel x para outra neste caso o u elevado a 15. eu tabem queria saber qunado eu preciso mudar a variavel do limite? desde ja muito obrigado rsrsrs, valeww mesmo cara,valeww tabem claudin!
eu entendi você igualou a divisão de u elevado a 15 / u-1 e o resultado . ai voce passou o divisor para outro lado multiplicando, ae assim ! não é a toa que você deve ser chamado de Professor parabens cara! Só para entender antes eu tinha o limite original, depois você me mostrou que alguns casos tem que mudar a varivel x para outra neste caso o u elevado a 15. eu tabem queria saber qunado eu preciso mudar a variavel do limite? desde ja muito obrigado rsrsrs, valeww mesmo cara,valeww tabem claudin!
