 por rafaelmtmtc » Dom Abr 19, 2009 12:56
por rafaelmtmtc » Dom Abr 19, 2009 12:56
Bom dia, tenho o seguinte problema:
Devo negar as situações:
Para todo numero real x, existe um numero natural n tal que n>x.
acho que a resposta seria:
Existe um numero real x para todo numero natural n tal que n<x
Existe um numero natural n tal que, para todo numero real x, tem-se n>x
acho que a resposta seria:
Existe um numero real x, tal que para todo numero natural n, tem-se n<x
Estou no caminho certo?
Obrigado
Rafael
-
rafaelmtmtc
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Sáb Abr 18, 2009 18:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: lic/bac matematica
- Andamento: cursando
 por Molina » Seg Abr 20, 2009 13:02
por Molina » Seg Abr 20, 2009 13:02
Bom dia, Rafael.
Faz tempo que não vejo isso profundamente, mas alguma coisa eu ainda lembro.
A negação de
PARA TODO (

) será
EXISTE UM (
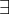
), e a negação de
EXISTE UM (
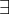
) será
PARA TODO (

).
Então acho que na sua segunda frase tem que fazer alguma mudança, concorda?
Abraços e bom estudo!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por rafaelmtmtc » Seg Abr 20, 2009 20:47
por rafaelmtmtc » Seg Abr 20, 2009 20:47
Acho que na segunda fiz isso, porém inverti a ordem das proposições, isto tem alguma interferência nos resultados ou não?
outra coisa, devo inverter o sentido de < e > quando faço o complementar, como fiz no exemplo no fininal da frase?
obrigado,
abrços
Rafael
-
rafaelmtmtc
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Sáb Abr 18, 2009 18:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: lic/bac matematica
- Andamento: cursando
 por Molina » Seg Abr 20, 2009 21:38
por Molina » Seg Abr 20, 2009 21:38
Boa noite, Rafael.
Isso mesmo, você tem que mudar o sinal de maior para menor ou vice-versa.
Cada frase você pode esquematizar com letras (p, q) que já tem o que deve ser feito para negá-la. Dá uma lida nesta página aqui e vê se você encontra o que deve ser feito em outras frases:
http://www.paulomarques.com.br/arq1-4.htmNao tinha percido que você tinha invertido as frases. Acho que está certa então!
Abraços!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por rafaelmtmtc » Seg Abr 20, 2009 22:04
por rafaelmtmtc » Seg Abr 20, 2009 22:04
Boa noite Molina,
muito obrigado mesmo.
Rafael
-
rafaelmtmtc
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Sáb Abr 18, 2009 18:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: lic/bac matematica
- Andamento: cursando
Voltar para Conjuntos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dúvida sobre operações entre conjuntos - complementar
por Fernanda Lauton » Sáb Out 09, 2010 21:18
- 3 Respostas
- 2627 Exibições
- Última mensagem por MarceloFantini

Sáb Out 09, 2010 23:18
Funções
-
- Conjunto vazio está dentro de outro conjunto vazio?
por JDomingos » Dom Jul 20, 2014 07:41
- 1 Respostas
- 2231 Exibições
- Última mensagem por DanielFerreira

Dom Jul 20, 2014 12:14
Conjuntos
-
- Conjunto
por Douglaspimentel » Qui Mar 18, 2010 16:52
- 4 Respostas
- 4326 Exibições
- Última mensagem por MarceloFantini

Qua Mai 12, 2010 13:49
Álgebra Elementar
-
- Conjunto
por aline2010 » Dom Jun 13, 2010 22:56
- 1 Respostas
- 1896 Exibições
- Última mensagem por Molina

Seg Jun 14, 2010 00:27
Álgebra Elementar
-
- CONJUNTO
por Douglaspimentel » Sex Dez 10, 2010 16:35
- 0 Respostas
- 1694 Exibições
- Última mensagem por Douglaspimentel

Sex Dez 10, 2010 16:35
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 ) será
) será 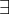 ), e a negação de
), e a negação de 


 .
.



