 por beel » Ter Out 04, 2011 22:45
por beel » Ter Out 04, 2011 22:45
derivada de f(x)= sen(x + x²)
seria, ( pela regra da cadeia)
sen'(x + x²)(x + x²)' =
cos(x + x²)(1 + 2x)*
minhas perguntas são:
1- o x² é uma função composta?
sua derivada ficaria apenas
* 2x ou seria 2x.(x)'
2- eu tenho que derivar a interna do cosseno? (x + x²)?
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por LuizAquino » Qua Out 05, 2011 11:25
por LuizAquino » Qua Out 05, 2011 11:25
isanobile escreveu:1- o x² é uma função composta?
sua derivada ficaria apenas
* 2x ou seria 2x.(x)'
Você até pode enxergar
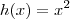
como uma função composta, mas isso é desnecessário. Basta aplicar direto a regra de derivação já conhecida para monômios:

.
Se ainda assim você quer enxergar uma composição de funções (e ter bem mais trabalho), então você poderia fazer algo como:
![f(u) = u^2 \textrm{ e } g(x) = x \Rightarrow h(x) = f(g(x)) = [g(x)]^2 = x^2 f(u) = u^2 \textrm{ e } g(x) = x \Rightarrow h(x) = f(g(x)) = [g(x)]^2 = x^2](/latexrender/pictures/9ef1549e8957c943bb3d678df95cd6b5.png)
Aplicando a Regra da Cadeia:

Mas, temos que:
(i)
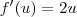
(ii)

(iii)

Portanto, no final ficamos com:
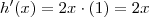
Obviamente, essa resposta é a mesma que já sabíamos!
isanobile escreveu:2- eu tenho que derivar a interna do cosseno? (x + x²)?
É claro que não!
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por beel » Sex Out 07, 2011 20:40
por beel » Sex Out 07, 2011 20:40
a resposta seria
cos(X + X²)(1+ 2X ) ?
Aaa não?eu sempre confundo isso na regra da cadeia,nao sei quando parar de derivar...
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por LuizAquino » Sáb Out 08, 2011 18:05
por LuizAquino » Sáb Out 08, 2011 18:05
isanobile escreveu:a resposta seria
cos(X + X²)(1+ 2X ) ?
Sim.
isanobile escreveu:eu sempre confundo isso na regra da cadeia,nao sei quando parar de derivar...
Se desejar revisar esse conteúdo, então eu recomendo que você assista a
vídeo-aula "13. Cálculo I - Regra da Cadeia".
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por beel » Dom Out 16, 2011 16:55
por beel » Dom Out 16, 2011 16:55
Ok,obrigada.
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [CALCULO] derivada de função composta 2
por beel » Ter Out 04, 2011 22:58
- 5 Respostas
- 3103 Exibições
- Última mensagem por beel

Qui Out 13, 2011 12:33
Cálculo: Limites, Derivadas e Integrais
-
- Derivada - função composta
por core » Qua Out 16, 2013 15:54
- 1 Respostas
- 1329 Exibições
- Última mensagem por Taka

Sáb Nov 02, 2013 21:12
Cálculo: Limites, Derivadas e Integrais
-
- Derivada de função composta
por Fernandobertolaccini » Qua Jul 09, 2014 08:37
- 0 Respostas
- 909 Exibições
- Última mensagem por Fernandobertolaccini

Qua Jul 09, 2014 08:37
Cálculo: Limites, Derivadas e Integrais
-
- derivada de função composta.
por nandooliver008 » Dom Set 21, 2014 19:42
- 1 Respostas
- 1220 Exibições
- Última mensagem por Cleyson007

Seg Set 22, 2014 18:04
Cálculo: Limites, Derivadas e Integrais
-
- Problema com a derivada de uma função composta
por DavidUserCalc » Qui Abr 01, 2010 14:44
- 1 Respostas
- 1944 Exibições
- Última mensagem por Molina

Qui Abr 01, 2010 16:56
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


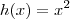 como uma função composta, mas isso é desnecessário. Basta aplicar direto a regra de derivação já conhecida para monômios:
como uma função composta, mas isso é desnecessário. Basta aplicar direto a regra de derivação já conhecida para monômios:  .
.![f(u) = u^2 \textrm{ e } g(x) = x \Rightarrow h(x) = f(g(x)) = [g(x)]^2 = x^2 f(u) = u^2 \textrm{ e } g(x) = x \Rightarrow h(x) = f(g(x)) = [g(x)]^2 = x^2](/latexrender/pictures/9ef1549e8957c943bb3d678df95cd6b5.png)

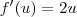


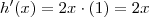

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.