Se a e b são números positivos, demonstre que a equação a seguir tem pelo menos uma solução no intervalo (-1, 1).
Cálculo 6 ed., James Stewart, p.117, q.62.
Já perdi horas com isso, e não há resposta em parte alguma. Como chutando valores de x no intervalo (-1, 1), geralmente se obtém parcelas negativas e, portanto, resposta negativa, minha estratégia foi tentar mostrar que ambas as parcelas são positivas num dado sub-intervalo dentro de (-1,1). Se eu conseguisse isto, mostraria que a função da esquerda (a soma à esquerda da igualdade, digo) varia entre valores negativos e positivos e, portanto, passa por zero - pois é uma função contínua e definida dentro do intervalo pedido.
No entanto fracassei.
Como a e b são positivos, cada parcela será positiva quando o denominador for positivo.
x³ + 2x² - 1 é positivo dentro do intervalo (-1,1) para 0.618 < x < 1.
* Esse 0.618 é aproximação de
![\frac{\sqrt[]{5}-1}{2} \frac{\sqrt[]{5}-1}{2}](/latexrender/pictures/9918704893c2bd1a0c876b26cac4a6df.png)
Mas x³ + x - 2 nunca é positivo dentro intervalo! Só para x > 1.
Então, aparentemente, eu precisaria mostrar que, nos casos em que a 1ª parcela é positiva (em 0.618 < x < 1), seu valor absoluto é às vezes maior que o da 2ª parcela negativa - o que faria a função ser positiva como preciso, rs. Acho que isso é demais pra mim, hehehe.
Imagino que a real solução seja mais simples, com outra estratégia.
Se alguém puder ajudar, ficaria grato.
Obrigado pela atenção.

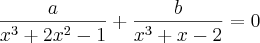

 e obteremos
e obteremos  . Agora considere esta relação no intervalo
. Agora considere esta relação no intervalo ![[-1,1] [-1,1]](/latexrender/pictures/d060b17b29e0dae91a1cac23ea62281a.png) , ou seja, fechado em -1 e 1. Quando
, ou seja, fechado em -1 e 1. Quando 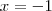 , nós temos
, nós temos 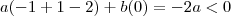 . Tomando
. Tomando  , teremos
, teremos 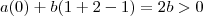 , logo pelo
, logo pelo  .
.

 Muito obrigado.
Muito obrigado.