 por SheylaTamarossi » Sáb Out 01, 2011 19:02
por SheylaTamarossi » Sáb Out 01, 2011 19:02
Olá... Estou com dúvida nesta questão, se puderem me ajudar...
Calcular a antiderivada de:
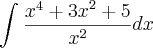
Devo integrar parte por parte, desse jeito?

Ou devo derivar a funçaõ toda?
-
SheylaTamarossi
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Dom Jun 12, 2011 10:50
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: 3° ano
- Andamento: cursando
 por Neperiano » Sáb Out 01, 2011 19:43
por Neperiano » Sáb Out 01, 2011 19:43
Ola
Assim, se for pra integra você pode fazer isso que você fez, se for pra deriva,dai tenque sera função toda, eu só fiquei na dúvida, o que é pra fazer, antiderivada de integral é derivada?
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por MarceloFantini » Dom Out 02, 2011 15:19
por MarceloFantini » Dom Out 02, 2011 15:19
A integral é a antiderivada, ou seja, basta resolver a integral. O que você fez está certo Sheyla, agora basta enxergar como polinômios.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Neperiano » Dom Out 02, 2011 16:23
por Neperiano » Dom Out 02, 2011 16:23
Ola
Tá mas o que seria, a antiderivada da integral?
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por MarceloFantini » Dom Out 02, 2011 16:26
por MarceloFantini » Dom Out 02, 2011 16:26
Você não entendeu. A antiderivada É a integral, ou seja, antiderivada=integral.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Neperiano » Dom Out 02, 2011 16:29
por Neperiano » Dom Out 02, 2011 16:29
Ola
Eu sei, mas pelo que foi postado pelo exercíco, dá a entender que é a antiderivada da integral
SheylaTamarossi escreveu:Olá... Estou com dúvida nesta questão, se puderem me ajudar...
Calcular a antiderivada de:
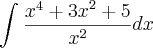
Devo integrar parte por parte, desse jeito?

Ou devo derivar a funçaõ toda?
Entende, eu sei que antiderivada é integral, mas pelo que está ali, parece outra coisa
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.













 , avisa que eu resolvo.
, avisa que eu resolvo.

