 por Claudin » Sáb Out 01, 2011 11:33
por Claudin » Sáb Out 01, 2011 11:33
Seja
f definida por
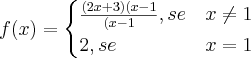
A resolução seria:
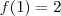
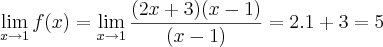
A função é descontínua no ponto x=1, porque em

, o resultado teria que ser também 2, como em x=1, correto?
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Renato_RJ » Sáb Out 01, 2011 15:27
por Renato_RJ » Sáb Out 01, 2011 15:27
Boa tarde Claudin, tudo em paz ??
Seguinte, a função será contínua se os limites laterais forem iguais, mas não necessariamente igual ao valor de x na função (a imagem de x). Para isso, faça o limite da função quando x tende a 1 pela esquerda e pela direita, se esses limites forem iguais, aí sim a função é contínua...
Abs,
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por Claudin » Sáb Out 01, 2011 20:06
por Claudin » Sáb Out 01, 2011 20:06
Tanto pela esquerda e pela direita o valor seria 5, o que difere de 2, que no caso quando x=1.
Ou seja, a função nao e continua, para ser continua o valor correto para os limites laterais deveria ser 2, correto?
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Renato_RJ » Dom Out 02, 2011 00:14
por Renato_RJ » Dom Out 02, 2011 00:14
Cuidado, o limite de uma função quando x tende a um valor não é, necessariamente, igual a imagem desse valor na função, isto é, se x = 1 implica em f(x) = 2, então o limite de f(x) quando x tende a 1 não é, necessariamente, 2...
Se os limites laterais são iguais (mesmo sendo diferente da imagem da função no ponto), então a função é contínua..
Abs,
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por Claudin » Dom Out 02, 2011 10:13
por Claudin » Dom Out 02, 2011 10:13
Não compreendi Renato
a definição de função continua nao seria
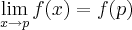
Portanto para a função ser continua os limites laterais teriam que ser iguais e o
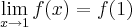
correto?
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Renato_RJ » Dom Out 02, 2011 14:34
por Renato_RJ » Dom Out 02, 2011 14:34
A função é dita contínua em um ponto quando seus limites laterais são iguais, isto é:
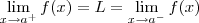
O seu argumento está correto, mas lembre-se do domínio onde a sua função está definida, um exemplo, use a definição de
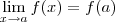
na função
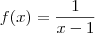
no ponto 1.. Você verá que ela é contínua em todo o domínio menos no ponto 1, pois seus limites laterais são diferentes...
Mas no seu exercício, quando x = 1 a f(x) = 2, mas quando

a sua função apresenta outra "cara", logo, para verificar se ela é contínua você teria que fazer o teste dos limites laterais, assim você poderá dizer se a função é contínua em todo o seu domínio (mesmo que a f(1) seja diferente do valor encontrado no limite).
Para melhor compreensão do que ocorre no limite, aconselho a ler sobre limites em algum livro de cálculo, tipo Stewart ou Apostol, lá verá que f(x) é diferente do limite em x, pois o limite expressa a ideia de "movimento na curva", tipo "o quão próximo estou de um valor L quando

"..
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por Claudin » Dom Out 02, 2011 14:54
por Claudin » Dom Out 02, 2011 14:54
Então a função é continua ou não?
No meu entendimento ela só seria contínua se a função no caso de x diferente de 1, tivesse a imagem 2, como no ponto x=1, a imagem é 2, ai sim seria contínua.
Deixe mais claro para mim.
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por MarceloFantini » Dom Out 02, 2011 15:23
por MarceloFantini » Dom Out 02, 2011 15:23
A função é
descontínua. Você está errando Renato. É verdade que não necessariamente o limite é o valor da função no ponto (pois ela pode nem estar definida), mas ela será contínua
se e somente se o limite for igual ao valor da função no ponto, ou seja, sempre que
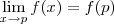
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Claudin » Dom Out 02, 2011 16:38
por Claudin » Dom Out 02, 2011 16:38
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Renato_RJ » Seg Out 03, 2011 02:25
por Renato_RJ » Seg Out 03, 2011 02:25
MarceloFantini escreveu:A função é
descontínua. Você está errando Renato. É verdade que não necessariamente o limite é o valor da função no ponto (pois ela pode nem estar definida), mas ela será contínua
se e somente se o limite for igual ao valor da função no ponto, ou seja, sempre que
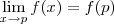
.
Opa, muito obrigado pela correção Marcelo...
Mil perdões Claudin...
[ ]'s
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por Claudin » Seg Out 03, 2011 10:37
por Claudin » Seg Out 03, 2011 10:37
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Continuidade Limite
por CaioLemos » Qui Mar 22, 2012 13:18
- 2 Respostas
- 2011 Exibições
- Última mensagem por CaioLemos

Qui Mar 22, 2012 17:39
Cálculo: Limites, Derivadas e Integrais
-
- Limite e Continuidade
por Thyago Quimica » Seg Mai 21, 2012 14:11
- 1 Respostas
- 1656 Exibições
- Última mensagem por LuizAquino

Ter Mai 22, 2012 19:22
Cálculo: Limites, Derivadas e Integrais
-
- Limite e Continuidade
por Raquel299 » Sex Abr 10, 2015 10:43
- 2 Respostas
- 1822 Exibições
- Última mensagem por Raquel299

Ter Abr 14, 2015 18:17
Cálculo: Limites, Derivadas e Integrais
-
- Limite e Continuidade
por Raquel299 » Ter Abr 14, 2015 20:58
- 1 Respostas
- 1467 Exibições
- Última mensagem por Cleyson007

Qua Abr 15, 2015 18:26
Cálculo: Limites, Derivadas e Integrais
-
- Limite- Continuidade em intervalos
por killerkill » Sáb Ago 13, 2011 02:25
- 7 Respostas
- 7918 Exibições
- Última mensagem por killerkill

Qua Ago 17, 2011 23:17
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 10 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
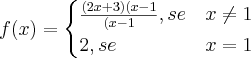
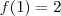
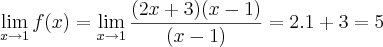
 , o resultado teria que ser também 2, como em x=1, correto?
, o resultado teria que ser também 2, como em x=1, correto?
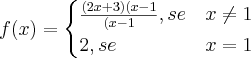
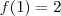
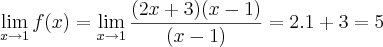
 , o resultado teria que ser também 2, como em x=1, correto?
, o resultado teria que ser também 2, como em x=1, correto?



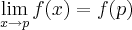
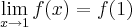

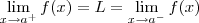
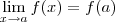 na função
na função 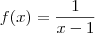 no ponto 1.. Você verá que ela é contínua em todo o domínio menos no ponto 1, pois seus limites laterais são diferentes...
no ponto 1.. Você verá que ela é contínua em todo o domínio menos no ponto 1, pois seus limites laterais são diferentes... a sua função apresenta outra "cara", logo, para verificar se ela é contínua você teria que fazer o teste dos limites laterais, assim você poderá dizer se a função é contínua em todo o seu domínio (mesmo que a f(1) seja diferente do valor encontrado no limite).
a sua função apresenta outra "cara", logo, para verificar se ela é contínua você teria que fazer o teste dos limites laterais, assim você poderá dizer se a função é contínua em todo o seu domínio (mesmo que a f(1) seja diferente do valor encontrado no limite). "..
"..

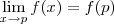 .
.


.




 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.