 por jorgeipu » Ter Set 27, 2011 08:57
por jorgeipu » Ter Set 27, 2011 08:57
Esta questão é do livro "MATEMÁTICA COMPLETA" de Giovanni e Bonjorno. (pág. 58 Q.09) - (UFMG) No triângulo ABC, o ângulo AbC é reto, BC=
![5\sqrt[]{6} 5\sqrt[]{6}](/latexrender/pictures/a8f117e9acfc82628102ca9b67fc2eda.png)
e cos(BÂC)=
![\frac{3}{\sqrt[]{15}} \frac{3}{\sqrt[]{15}}](/latexrender/pictures/7e74f473dea9567638c3fe95c97fad1b.png)
Considerando esses dados, calcule o comprimento do cateto AB.
A resposta é pra ser AB=15. Já tentei resolver mas acho que falta alguma informação
-
jorgeipu
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Set 27, 2011 08:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: formado
 por Renato_RJ » Ter Set 27, 2011 14:11
por Renato_RJ » Ter Set 27, 2011 14:11
Vamos ver se posso lhe ajudar, campeão...
Seguinte, o
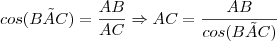
Usando o teorema de Pitágoras (pois o triângulo é reto), temos:
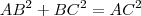
Logo temos:
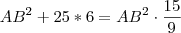
O que nos dá:
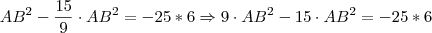
Multiplicando ambos os lados por -1, para garantir medidas reais, temos:
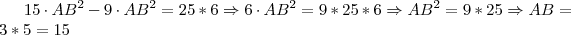
Espero ter ajudado...
[ ]'s
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por jorgeipu » Qua Set 28, 2011 11:52
por jorgeipu » Qua Set 28, 2011 11:52
Renato_RJ escreveu:Vamos ver se posso lhe ajudar, campeão...
Seguinte, o
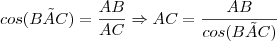
Usando o teorema de Pitágoras (pois o triângulo é reto), temos:
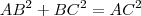
Logo temos:
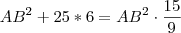
O que nos dá:
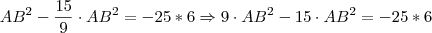
Multiplicando ambos os lados por -1, para garantir medidas reais, temos:
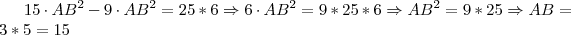
Espero ter ajudado...
[ ]'s
Renato.
Valeu irmão!!!
Ajudou e muito
Jorge Fernando
-
jorgeipu
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Set 27, 2011 08:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [trigonometria] trigonometria em triangulo qualquer
por biamassa00 » Sex Mai 25, 2012 22:19
- 0 Respostas
- 3598 Exibições
- Última mensagem por biamassa00

Sex Mai 25, 2012 22:19
Trigonometria
-
- (Trigonometria) problema trigonometria
por Luizap11 » Qui Dez 05, 2013 00:33
- 2 Respostas
- 5277 Exibições
- Última mensagem por Edunclec

Qui Dez 05, 2013 20:53
Trigonometria
-
- trigonometria
por Cleyson007 » Qua Set 24, 2008 19:44
- 2 Respostas
- 3419 Exibições
- Última mensagem por admin

Ter Set 30, 2008 19:08
Trigonometria
-
- trigonometria
por Micheline » Dom Jan 25, 2009 16:21
- 5 Respostas
- 4972 Exibições
- Última mensagem por Cleyson007

Seg Jan 26, 2009 17:27
Trigonometria
-
- Trigonometria
por Flavio » Sex Fev 13, 2009 21:29
- 5 Respostas
- 5134 Exibições
- Última mensagem por Molina

Seg Fev 16, 2009 01:53
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![5\sqrt[]{6} 5\sqrt[]{6}](/latexrender/pictures/a8f117e9acfc82628102ca9b67fc2eda.png) e cos(BÂC)=
e cos(BÂC)= ![\frac{3}{\sqrt[]{15}} \frac{3}{\sqrt[]{15}}](/latexrender/pictures/7e74f473dea9567638c3fe95c97fad1b.png)

![5\sqrt[]{6} 5\sqrt[]{6}](/latexrender/pictures/a8f117e9acfc82628102ca9b67fc2eda.png) e cos(BÂC)=
e cos(BÂC)= ![\frac{3}{\sqrt[]{15}} \frac{3}{\sqrt[]{15}}](/latexrender/pictures/7e74f473dea9567638c3fe95c97fad1b.png)

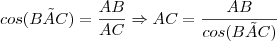
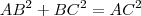
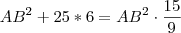
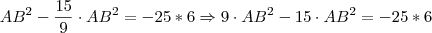
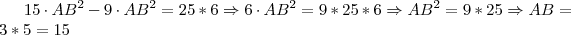


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
