"Considerando-se as funções reais
 (uma observação, é 2 elevado a (x+1)... nao consegui fazer isso )e
(uma observação, é 2 elevado a (x+1)... nao consegui fazer isso )e  , é correto afirmar:
, é correto afirmar: (01) A equação (tex) gof(x) = 0 (/tex) possui uma única raiz igual a
 ."
."A afirmativa é verdadeira, questão estilo UFBA... A propósito, não achei em canto nenhum como colocar o 2 na base do log... ou seja o dois é a base e o que está entre parenteses, o logaritmando.
A primeira vez que tentei fiz de um modo completamente errado... A segunda, achei que
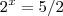 mas essa, obviamente não é a resposta :X
mas essa, obviamente não é a resposta :XAjuda?

p.s.: desculpem os erros de formatação com o LaTex , sou nova aqui e nao encontrei nos fóruns as formatações desejadas.


 . Para escrever subscrito:
. Para escrever subscrito: . Sobre a questão, vamos analisar: encontrando a composta:
. Sobre a questão, vamos analisar: encontrando a composta: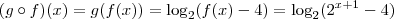
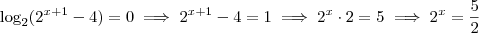
 . Aplicando o logaritmo na base 2 dos dois lados:
. Aplicando o logaritmo na base 2 dos dois lados: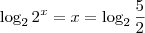



![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)